Effet Sagnac - Définition

Un problème plus compliqué qu'il n'y paraît

En plus des paradoxes soulevés dans les sections précédentes et du problème de l'universalité de l'effet Sagnac, récapitulons quelques remarques qui montrent que le raisonnement simpliste est faux ou, à tout le moins, qu'il doit être sérieusement mis en doute et que l'analyse de l'effet Sagnac en relativité restreinte nécessite un traitement plus rigoureux.

• Dans l'espace-temps les rayons lumineux ne suivent pas la même trajectoire.
  
  Même dans R les trajectoires sont différentes, bien que dans R, la situation des deux trajectoires soit totalement symétrique et aucun problème particulier ne se pose.
  Ce dessin peut être trompeur car en relativité restreinte l'espace-temps est de Minkowski et pas euclidien comme cette figure. Il faut donc faire attention.
• Dans R', il y a asymétrie de ces trajectoires à cause de la rotation. Cette asymétrie n'existe pas dans R. C'est la différence entre R et R'.
• On ne peut pas considérer la circonférence vue dans le repère R comme la longueur des trajectoires dans R', même en lui appliquant la contraction des longueurs, car on ne peut pas sans précaution séparer l'espace du temps (l'espace en relativité restreinte n'est pas absolu) et l'existence de deux trajectoires asymétriques dans l'espace-temps ne simplifie pas les choses.
  Dans le dessin, la partie spatiale est l'horizontale (la longueur des circonférences est indiquée), identique pour les deux trajectoires, mais, répétons-le, la figure « sur papier » obéit à la géométrie d'Euclide, tandis que l'espace-temps à l'étude est de Minkowski, compliqué ici par la rotation.
  Ce problème peut-être relié aux intervalles de type spatial. Cet intervalle n'ayant pas de signification physique (pas de lien causal), la longueur de l'intervalle n'est pas fixée a priori. Lui attribuer une valeur quelconque ou le considérer comme non invariant ne modifie pas la physique. C'est une simple considération mathématique. Ce n'est que des considérations en rapport avec le principe de relativité qui conduisent à la forme de l'intervalle invariant, y compris spatial, que nous connaissons. Si l'on ne tenait compte que des données physiques (l'invariance de la vitesse de la lumière dans le vide), nous aurions plus de liberté et même si les intervalles lumineux et temporels seraient toujours invariants, l'intervalle spatial pourrait être quelconque.
  La circonférence est la longueur d'une figure géométrique purement spatiale. Par conséquent, on ne peut pas, sans précaution, considérer que la longueur des trajectoires est numériquement égale à la circonférence. Il pourrait y avoir violation involontaire du principe de relativité.
  L'espace n'est pas absolu. La relativité restreinte nous enseigne que tout est relatif et que la physique doit se décrire par les relations entre observateurs et objets. Le choix du repère n'est là que pour donner des valeurs numériques aux variables. On ne peut pas considérer le dessin avec le cercle comme un cadre absolu qui permettrait de mesurer à coup sûr la longueur des trajectoires.
• Les rayons lumineux ne suivent pas les géodésiques (c'est-à-dire les chemins les plus courts).
  Appelons A et B les points où O' rencontre les deux signaux lumineux. Traçons les géodésiques dans R (une droite) et dans R'.
  
  Pourquoi la géodésique ne rejoint-elle pas B dans R' ? Parce que les deux évènements spatio-temporels A et B ne peuvent pas être joint par une géodésique lumineuse (la lumière se déplace beaucoup plus vite que O' et les deux ratent leur rencontre). Par conséquent, A et B sont confondus dans R' (puisque O' est immobile dans R'), mais la géodésique lumineuse, la ligne droite dans R, est vue comme courbe dans R'. Pour s'en convaicre, dessiner cette géodésique point par point à partir de celle dans R en tenant compte de la vitesse c et de la vitesse et de la rotation de O' (par exemple en utilisant du papier millimétré et une calculette).
  Les trajectoires lumineuses entre A et B (évènements spatio-temporels) ne sont pas des géodésiques lumineuses et ne sont donc pas les chemins les plus courts dans l'espace-temps. La lumière doit emprunter une trajectoire imposée grâce à des miroirs ou une fibre optique, justement à cause de cela.
  Étant donné l'asymétrie des trajectoires, on ne peut pas supposer, sans le vérifier, que ces deux trajectoires « allongées » ont la même longueur dans l'espace-temps. Quand on voit la géodésique dans R', ce n'est pas trivial.
  Les géodésiques sont les chemins les plus courts, par exemple dans un espace plat (une feuille de papier) ,elles forment le quadrillage de la feuille. Sur une sphère, ce sont des courbes (les méridiens, par exemple).
  Cette courbure de la géodésique montre que l'espace est courbe dans R'. Même en physique classique (espace euclidien), l'espace est courbe vu dans un repère accéléré. Mais cela est peu discuté, car :
  • On sait qu'on doit s'appuyer sur un espace de Minkowski, donc on préfère passer directement à des espaces courbes relativistes.
  • Si on reste dans la physique classique, galiléenne, on peut se passer de ces subtilités en raisonnant dans R pour la cinématique et en utilisant, dans R', des astuces du type « forces fictives » ou « dérives » (force centrifuge et force de Coriolis responsable du sens de rotation des cyclones et due à la rotation de la Terre). L'espace-temps euclidien autorise des facilités que l'on n'a pas avec l'espace-temps de Minkowski.
• La courbure d'une variété (une ligne, une surface, etc.) est une propriété locale intrinsèque. Par exemple, on ne peut faire disparaître la courbure d'une sphère en l'aplatissant : elle se déchire.
  Il ne faut pas la confondre avec la courbure extrinsèque imposée de l'extérieur, par exemple en roulant une feuille de papier en cylindre : cela ne modifie pas la feuille de papier, seulement la manière dont elle est vue.
  Dans la suite du texte, quand on parlera de courbure, ce sera toujours de courbure intrinsèque.
  Le paradoxe d'Ehrenfest a déjà présenté ce type d'espace courbe (espaces sphériques ou hyperboliques) où la géométrie n'est pas euclidienne.
  Or l'espace-temps de Minkowski est plat (les trajectoires les plus courtes sont des droites). Un changement d'observateur ne modifie pas la courbure de l'espace-temps. La courbure peut d'ailleurs s'exprimer de manière mathématiquement invariante pour tout observateur.
  L'espace-temps dans R' doit donc rester plat. Ce n'est qu'en relativité générale que l'espace-temps est considéré courbe. Par des raisonnements simples, en présence de la gravitation, l'espace-temps ne peut pas rester plat.
  Mais ici nous n'envisageons nullement la gravitation. Nous avons un repère inertiel R dans un espace-temps plat de Minkowski et un observateur O' qui suit une trajectoire courbe (un cercle).
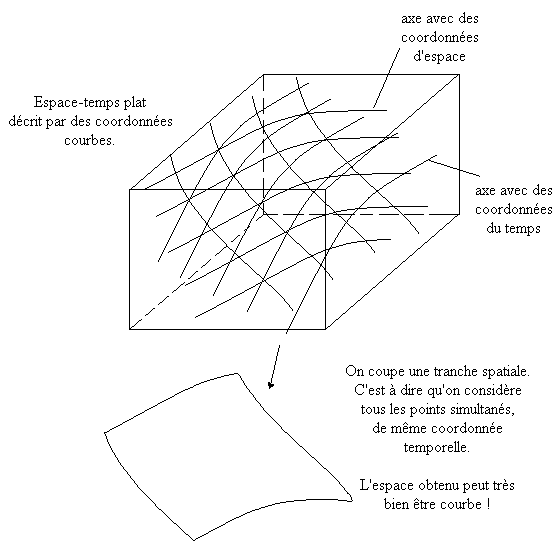
  Mais avoir un espace-temps plat ne signifie pas que l'espace est plat. Les géodésiques étant courbes, on doit employer des coordonnées curvilignes. Et si l'on effectue une « coupe » dans l'espace-temps pour considérer une « tranche » d'espace (on considère tous les points simultanés dans un repère donné), cette tranche ne sera pas nécessairement plate.
  C'est vrai en géométrie euclidienne, la plus communément apprise : il est donc difficile d'imaginer qu'il puisse en être autrement. Mais en géométrie de Minkowski, on ne peut pas séparer l'espace et le temps de manière arbitraire. Le problème étant que ce sont toutes les coordonnées qui sont curvilignes, y compris le temps.
  
  
• Une analogie avec une autre expérience donne un indice sur l'origine de la difficulté.
  Plaçons O et O' sur un segment de droite terminé par des miroirs.
  
  Cette expérience est identique à celle de Sagnac sauf que les rayons lumineux font demi-tour sur des miroirs au lieu de faire le tour sur un cercle.
  Ici aussi O' va constater un décalage et une vitesse apparente (en utilisant la longueur du segment pour calculer la vitesse) anisotrope.
  La longueur des trajectoires, même pour ce qui est de l'espace seul, est différente aussi bien dans R que dans R', et les miroirs se déplacent par rapport à O'.
  Se pourrait-il que dans l'expérience Sagnac, il y ait un phénomène analogue ? Dans la figure ci-dessus, on pourrait demander à ce que les rayons lumineux fassent un aller-retour avec les deux miroirs, ce qui est équivalent à un tour sur le cercle. Dans ce cas, cette figure est la projection sur une droite de l'expérience de Sagnac.

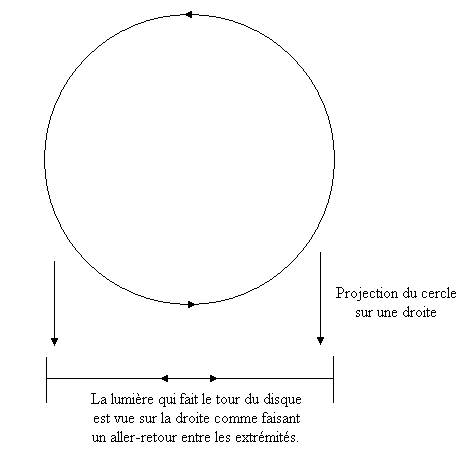
L'effet Sagnac est indépendant du rayon de courbure et on peut faire tendre l'arc de cercle de O' vers un segment de droite.
Dans ce cas, on devrait aussi considérer que pour R', la longueur des trajectoires n'est pas la même.
Quel est l'équivalent du déplacement des miroirs par rapport à O' dans le cas de l'expérience de Sagnac ? En fait, les miroirs fixent la géométrie de la trajectoire des rayons lumineux. Dire que les miroirs changent, que les trajectoires changent ou que la géométrie décrite par ces trajectoires change revient au même. Le changement de géométrie a une cause physique : l'accélération centripète. Dans le cas de l'expérience de Sagnac, cela devrait se traduire par un changement dans la géométrie avec une symétrie par rotation. C'est un peu plus compliqué à étudier qu'une situation linéaire avec deux miroirs.