Effet Sagnac - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Introduction et présentation succincte - Interprétation simpliste - Présentation détaillée - Un problème plus compliqué qu'il n'y paraît - L'addition des vitesses - Résultats expérimentaux récents

Interprétation simpliste

Dans cette section, l'effet Sagnac est interprété de façon simpliste dans un paradigme relativiste. Bien que cette interprétation mène à des résultats désastreux, elle a le mérite d'exposer plusieurs notions importantes.

Dans le référentiel R de O, les deux signaux arrivent sur O' avec un décalage $Δ t$ mesuré sur l'horloge de O. O', en mouvement, doit observer une dilatation du temps. Toutefois, ce n'est pas si simple car O' se déplace entre les deux réceptions des signaux. Sachant que le temps dépend aussi de la position, il faut utiliser les transformations de Lorentz.

Supposons que la vitesse de rotation du disque n'est pas trop grande pour pouvoir assimiler la trajectoire de O' (entre l'émission et les réceptions des signaux) à un segment de droite. Ainsi, l'utilisation des transformations de Lorentz semble être justifiée.

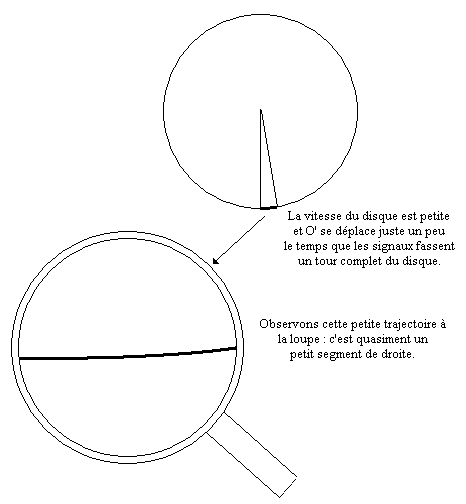
Les signaux seront reçus par O' (dans le repère R) aux coordonnées :

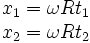
On peut alors appliquer les transformations de Lorentz :

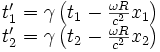
Soit avec les coordonnées précédentes :

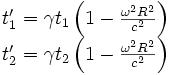
\begin{matrix}t'_1=\gamma t_1\left(1-\frac{\omega^2R^2}{c^2}\right)\\t'_2=\gamma t_2\left(1-\frac{\omega^2R^2}{c^2}\right)\end{matrix}

On trouve donc dans le repère R' de O' :

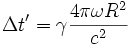
Le résultat trouvé, c'est-à-dire le décalage de temps d'arrivée des deux signaux sur O' dans R', est exactement la valeur approchée obtenue précédemment, à un facteur gamma près (alors que pour cette expression approchée, nous sommes partis de la valeur classique exacte). Habituellement, c'est plutôt l'inverse qui se produit (la formule relativiste redonne la formule classique en supposant gamma proche de 1, en négligeant les termes d'ordres supérieurs, proportionnels au carré de la vitesse, comme dans le cas de l'effet Doppler).

Pour calculer la vitesse du signal dans R', il faut connaître la longueur de la circonférence. A priori, ce n'est pas trivial, car dans R la contraction des longueurs ne s'applique pas de manière homogène selon le point considéré sur la circonférence (l'orientation de la vitesse varie avec l'angle).

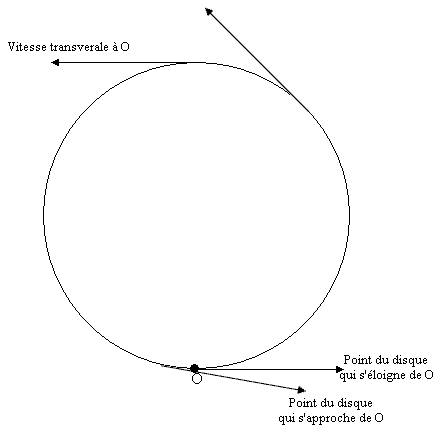
Mais grâce à la symétrie par rotation, il y a plus simple. En effet, à cause de cette symétrie, dans R et R', un disque reste un disque. La géométrie reste inchangée (ce raisonnement est incorrect). Par conséquent la contraction doit être homogène. De plus, la circonférence étant forcément toujours tangente à la vitesse, la contraction de Lorentz est indépendante de l'angle (ce qui est contradictoire avec ce qui est écrit auparavant, mais de toute façon, une contraction variable, donnant une circonférence bizarre, ne ferait que donner un facteur correctif en plus du facteur gamma, cela ne changerait pas les conclusions).

Si le disque a le périmètre $2π R'$ dans R' (le disque est immobile dans ce repère, ne pas confondre les repères R et R' avec les rayons du disque dans ces deux repères $R$ et $R'$ ), alors il aura une longueur plus courte d'un facteur gamma dans R. $2π R = 2π R' / γ$ . C'est-à-dire que dans R' la longueur parcourue est plus longue.

Comme la vitesse des signaux est obtenue en divisant cette longueur par le temps de parcours et comme les deux sont augmentés d'un facteur gamma, il y a compensation. Un petit calcul utilisant les transformations de Lorentz pour la position et les coordonnées temporelles ci-dessus montrent que les formules d'addition des vitesses trouvées dans le cas classique restent valables :

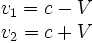
(où $V = ω R$ est la vitesse au bord du disque, c'est-à-dire la vitesse angulaire fois le rayon, la vitesse angulaire étant le nombre de tours par seconde multiplié par deux pi).