Effet Sagnac - Définition

Présentation détaillée

Description du phénomène

L'effet Sagnac consiste à émettre, en même temps et en sens inverse, deux signaux lumineux à l'aide d'un émetteur-récepteur fixé sur un disque tournant, en les contraignant à suivre la périphérie du disque tournant, puis à mesurer le décalage temporel entre les instants de réception de ces deux signaux sur l'émetteur-récepteur. Pour bien comprendre, il est utile de comparer ce cas à celui ou les deux signaux sont envoyés et reçus par un observateur O au repos dans le repère inertiel où tourne le disque.

Un observateur O immobile envoie deux signaux 1 et 2 autour d'un disque de rayon R en rotation à la vitesse angulaire ω. Chaque signal fait le tour du disque.

Pour cela, on peut utiliser des miroirs, des fibres optiques ou d'autres dispositifs.

Il existe bien d'autres configurations possibles, par exemple employant des fibres optiques, avec des sources en rotation ou pas et des détecteurs interférométriques en rotation ou pas. On peut aussi faire interférer les deux rayons sur l'anneau lui-même de manière à obtenir une onde stationnaire en utilisant deux faisceaux de fréquences légèrement différentes. Cela peut se faire automatiquement en intégrant la cavité laser dans le circuit et en renvoyant les faisceaux dans la cavité après un tour. Ces dispositifs à verrouillage de phase sont les plus précis.

Revenons à la disposition circulaire. Nous supposerons dans un premier temps que ce sont deux signaux lumineux se propageant à la vitesse c (comme dans le vide).

Pour le moment, la rotation du disque n'a pas d'importance. Les deux signaux partis simultanément de O reviennent, après un tour, en O en même temps.

Considérons maintenant un observateur O' situé en périphérie du disque et en rotation avec celui-ci. Nous choisissons O' pour qu'il soit en O au moment où les deux signaux sont émis.

Comme O' se déplace, lorsque les signaux se rencontrent en O, O' n'est plus au même endroit. O' va à la rencontre du signal 2 qui arrive en O' un peu plus tôt et il fuit le signal 1 qui arrive en O' un peu plus tard.

Voyons ce qui se passe dans le repère de O', c'est-à-dire du point de vue de O'.

Dans le repère de O', le disque n'est pas en rotation (O' est immobile dans son propre repère et il est solidaire du disque). Les deux signaux font le tour et se retrouvent en O' après un tour. Mais contrairement au cas de la première figure, comme nous venons de le voir, les deux signaux n'arrivent pas en même temps. Le signal 1 arrive après le signal 2. Pour O', le signal 2 est plus rapide que le signal 1. La vitesse apparente des signaux est anisotrope (différente selon le sens de rotation du signal).

L'emploi du terme "apparent" est important car ce qui est mesuré n'est pas directement une vitesse mais les temps de départ et d'arrivée des signaux (ou un déplacement des franges d'interférence dans le cas d'une mesure interférométrique). Nous n'avons pas mesuré la longueur du parcours. Bien sûr, il semble évident que cette longueur soit simplement la longueur du cercle. Mais en relativité restreinte ce n'est pas aussi simple ! Ce qui n'empêche pas de nombreux amateurs de relativité de faire cette confusion facile.

Voyons maintenant, en physique classique (non relativiste, c'est-à-dire en utilisant les transformations de Galilée), ce que valent ces vitesses apparentes et le décalage de temps d'arrivée des signaux.

La vitesse angulaire du signal lumineux est simplement c / R. Par conséquent, si on appelle t₁ et t₂ les temps mis par les signaux 1 et 2 pour rencontrer à nouveau O', nous avons :

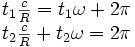
Soit

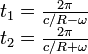
Nous trouvons donc pour le décalage de temps d'arrivée des signaux en O' :

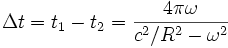
Si la vitesse angulaire du disque (ou ce qui revient au même du repère en rotation) est faible par rapport à la vitesse angulaire de la lumière (régime non relativiste), alors

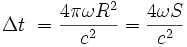
où S est la surface du disque.

Pour calculer la vitesse apparente des signaux pour O' (dans son repère), il suffit de diviser la circonférence par le temps de parcours. Cela donne les vitesses apparentes des deux signaux :

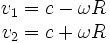
Si l'on note V la vitesse tangentielle du disque (ou de O' ou du repère en rotation), on a :

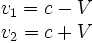
On trouve que la vitesse, dans le repère de O', des deux signaux est :

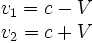
où V est la vitesse de O' dans R (la vitesse tangentielle au disque).

Ce qui est, sommes toute, bien naturel puisque nous retrouvons l'addition des vitesses de Galilée.

Résultats expérimentaux

L'effet a d'abord été constaté et mesuré en analysant les franges d'interférences des signaux lumineux en O'. Depuis, l'utilisation de laser, d'horloges atomiques et d'autres dispositifs, permet d'autres mesures et en particulier la mesure directe du décalage temporel (la différence de temps d'arrivée des signaux en O') calculé ci-dessus.

En 1893 Sir Oliver Lodge proposa d'étudier les effets de la rotation de la terre avec un grand interféromètre. Puis, en 1897, il proposa d'utiliser des interféromètres sur un disque en rotation. L'effet fut théoriquement anticipé par Michelson en 1904. En 1913, Sagnac a vérifié ces prédictions en utilisant un interféromètre en rotation rapide. Il avait prédit les résultats ci-dessus dans le cadre de la physique classique. Ce fut aussi le premier résultat expérimental rapporté de ce qui fut nommé l'effet Sagnac.

Toutefois, cet effet fut détecté par Franz Harres en 1912 dans une expérience de Fizeau, mais il ne fut correctement interprété comme étant l'effet Sagnac qu'en 1914 par Harzer.

En 1925, Michelson et Gale mesurèrent la rotation de la terre grâce à un grand interféromètre.

Depuis les années soixante, des mesures de plus en plus précises ont pu être effectuées grâce à l'emploi des lasers.

Les gyrolasers Sagnac (des gyroscopes à laser exploitant l'effet Sagnac) sont couramment utilisés pour mesurer avec précision la rotation d'un dispositif (relativement à un repère inertiel).

Universalité

Les formules précédentes restent valables pour un signal à vitesse quelconque (à condition de remplacer c par la vitesse du signal, étant entendu que c'est la vitesse du signal mesurée dans le repère R).

Mais ce que l'on désire mesurer, ce n'est pas le décalage entre O et O' (la dernière formule avec les vitesses apparentes traduit simplement l'addition galiléenne des vitesses), mais l'éventuel décalage de deux signaux émis dans un repère en rotation (c'est-à-dire avec la vitesse des signaux mesurée par O', la vitesse « normale », mesurée localement, pas en la regardant faire un tour). On désire considérer ce qui se passe réellement dans ce genre de repère, indépendamment de ce que fait O.

Si on emploie autre chose que de la lumière dans le vide, il faut veiller à ce que ce soit O' qui envoie lui-même les signaux afin qu'ils aient localement (en principe) la même vitesse dans R' (comme c'est le cas de la lumière en relativité dont la vitesse est invariante), le repère de O'. Et pour la lumière, un milieu de propagation en rotation si sa vitesse dans ce milieu est inférieure à c (par exemple des fibres optiques fixées au disque, car dans ce cas la vitesse du milieu influence la vitesse du signal, comme dans le cas du son avec l'air, ce que l'on vérifie aisément en mesurant la vitesse du signal sur un aller-retour dans de l'eau en mouvement, comme dans l'expérience de Fizeau).

Mais si c'est O' qui envoie le signal, aucun décalage ne peut être prédit par la méthode précédente. Dans O', les deux signaux allant à même vitesse, comme on le voit sur la figure tracée dans le référentiel de O', les deux signaux arriveront en même temps (c'est pour O qu'ils seront décalés). Comme dans la figure ci-dessus, ils parcourent le même cercle à la même vitesse, même si c'est dans des sens différents, et ils doivent arriver en O' en même temps.

En réalité un décalage est bien constaté. Et, plus surprenant encore, le décalage (de temps) calculé précédemment est identique quelle que soit la nature du signal et sa vitesse. C'est ce que l'on appelle l'universalité de l'effet Sagnac.

Cet effet est donc difficile à expliquer en physique classique (avec les transformations de Galilée, c'est même impossible).

Déjà, en 1914, Harzer avait constaté que l'effet subsiste en présence de la réfraction, c'est-à-dire dans un milieu où la lumière va moins vite que c.

L'effet avec des signaux de « matière » fut vérifié plus tard :

• En 1965, Zimmermann et Mercerau utilisèrent des paires de Cooper.
• En 1984, Atwood utilisa des neutrons.
• En 1991, Riehle utilisa des atomes de calcium.
• Et en 1993, Hasselbach et Nicklaus utilisèrent des électrons.
• L'effet de la rotation terrestre avec des neutrons fut mesuré par Werner an 1979.

Le problème de la lumière

En plus du problème de l'universalité, en relativité restreinte un problème supplémentaire se pose. En effet, en relativité restreinte, la vitesse de la lumière dans le vide est invariante et isotrope. Or les raisonnements qui ont conduit aux vitesses apparentes dans ce qui précède sont qualitativement indépendants de la relativité (un facteur gamma pourrait intervenir, tout au plus). Le raisonnement effectué avec les signaux émit par O et le décalage observé par O' (car il s'est déplacé le temps que les signaux fassent le tour) ne semble pas dépendre de la relativité restreinte.

Rappelez-vous la figure plus haut et le raisonnement effectué :

Ce décalage est évident, inévitable. L'anisotropie de la vitesse de la lumière (émise par O) semble donc incontournable dans un repère tournant (celui de O'). Ennuyeux pour une théorie (la relativité restreinte) qui dit que la vitesse de la lumière est invariante et isotrope !

Ce fait a plusieurs fois été utilisé pour tenter de réfuter la relativité restreinte, même encore récemment, aussi bien par des amateurs de relativité que par des théoriciens ayant en principe des connaissances plus approfondies de la relativité restreinte.

En réalité l'effet Sagnac est compatible avec la relativité restreinte et l'isotropie de la vitesse de la lumière dans tout repère mais que la relativité restreinte prédit en plus l'universalité du phénomène.

La déduction des transformations de Lorentz est valable dans tout repère (y compris accéléré) mais uniquement de manière locale dans un repère accéléré (c'est-à-dire dans un voisinage infinitésimal de l'origine du repère et pendant une durée infinitésimale). La vitesse de la lumière est peut-être invariante et isotrope localement, mais qui dit que sur un tour complet cela reste vrai ? Évidemment vous devez certainement vous demander comment cela est possible, comment une vitesse invariante en tout point peut donner quelque chose de variable sur une distance finie (la moyenne d'une valeur constante est égale à cette valeur). Ou comment la même vitesse locale pourrait conduire à une vitesse globale différente selon le sens de parcours du disque (la circonférence ne dépend pas du sens dans lequel on considère le cercle). Il y a effectivement des choses bien étranges qui se passent et, par exemple, définir le repère en rotation de tout le disque pose de grosses difficultés.

Mais ne brûlons pas les étapes, avant d'attaquer le problème correctement, rigoureusement et dans toute sa généralité, présentons une dérivation relativiste "simpliste" ainsi qu'une série de paradoxes liés à l'effet Sagnac.