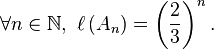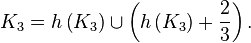Ensemble de Cantor - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
L'ensemble de Cantor a de nombreuses propriétés particulières.
Mesure
L'ensemble de Cantor est de mesure nulle, c'est-à-dire négligeable au sens de la mesure de Lebesgue.
En effet en notant
-
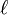
![\ell \left( [0,1] \right) = 1](https://static.techno-science.net/illustration/Definitions/autres/c/ca8b11a47879535bf014a8a342f4da1b_ab54c26341e946f4d5ec55f9ecee9356.png)
- pour une réunion An d'intervalles :
![\ell \left( [0,1] \right) = 1](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/ca8b11a47879535bf014a8a342f4da1b_ab54c26341e946f4d5ec55f9ecee9356.png)
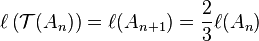
où
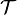
On en déduit que pour les étapes de la construction itérative ci-dessus :
Et comme l'ensemble de Cantor est inclus dans tous les An :
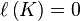
L'ensemble de Cantor est donc « petit » au sens de la mesure de Lebesgue.
Non-dénombrabilité
Cependant l'ensemble de Cantor n'est pas dénombrable ; il a la puissance du continu (voir Infini).
En effet, on peut montrer que les ensembles K3 et [0,1] sont équipotents.
Pour cela on associe à tout élément
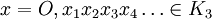
![f(x)=0,x'_1 x'_2 x'_3 x'_4 \ldots \in [0,1]](https://static.techno-science.net/illustrationWebp/Definitions/autres/1/19d19b681e3fb7b504cd089840eb2ee8_96d89ae21891965c4ef6180e9280e50f.png)
- x'i = 0 si xi = 0 ;
- x'i = 1 si xi = 2.
Par exemple l'élément
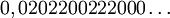
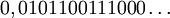
Il est facile de voir que cette application est surjective mais non injective (l'élément 0,1 étant l'image de
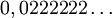
On peut aussi utiliser l'écriture en base 3. Celle-ci montre que K3 est équipotent à
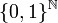
Ainsi l'ensemble de Cantor est « grand » au sens de la théorie des ensembles.
Propriétés topologiques
- L'ensemble de Cantor est compact, et n'a que des points d'accumulation. On dit que c'est un ensemble parfait. Par ailleurs, il est d'intérieur vide,
Soit P un point de K3, et soit une boule ouverte (intervalle ouvert) centrée en P. Cet ouvert contient nécessairement un réel dont le développement en base 3 contient le chiffre 1, qui n'est pas élément de K3. Donc P n'est pas intérieur à K3. Par ailleurs, dans ce même intervalle, il existe toujours un réel dont le développement en base 3 s'écrit uniquement avec des 0 ou des 2. Donc P n'est pas un point isolé.
- L'ensemble de Cantor est également totalement discontinu c'est-à-dire que chaque singleton est sa propre composante connexe, et homéomorphe à l'espace topologique
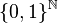
- Enfin l'ensemble de Cantor est « universel dans la catégorie des espaces métriques compacts», autrement dit tout espace métrique compact est l'image de l'ensemble de Cantor par une application continue. Cette affirmation a des répercussions importantes en analyse fonctionnelle.
Auto-similarité
L'image de l'ensemble de Cantor par l'homothétie h de centre 0 et de rapport 1/3 est elle-même une partie de l'ensemble de Cantor. Plus précisément
Ainsi, K3 est la réunion disjointe de deux parties qui lui sont homothétiques. C'est une manifestation de ce qu'on appelle l'auto-similarité, qui est l'une des propriétés de base des fractales.
Dimension
En conséquence de ce qui précède, on peut calculer la dimension de Minkowski ; elle vaut log(2)/log(3), nombre réel compris entre 0 et 1. On parle parfois de dimension fractionnaire car elle n'est pas entière, même s'il ne s'agit pas davantage d'un nombre rationnel. Dans cette formule, peu importe qu'on interprète log comme logarithme naturel ou logarithme décimal. On peut aussi écrire que la dimension vaut log3(2) (logarithme de 2 en base 3).
Cette valeur est également la dimension de Hausdorff de l'ensemble. On peut donc dire que l'ensemble de Cantor est de dimension log(2)/log(3) sans se soucier de la dimension utilisée.
