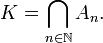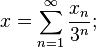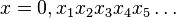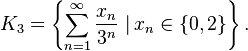Ensemble de Cantor - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, l'ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous-ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor.
Il s'agit d'un ensemble fermé du segment [0,1], d'intérieur vide. Il sert d'exemple pour montrer qu'il existe des ensembles infinis non dénombrables mais négligeables au sens de la mesure de Lebesgue. C'est aussi le premier exemple de fractale (bien que le terme ne soit apparu qu'un siècle plus tard), et il possède une dimension non-entière (voir plus bas).
Il admet enfin une interprétation en termes de développement des réels en base 3. Pour cette raison, il est souvent noté K3.
On le construit de manière itérative à partir du segment [0,1] en enlevant le tiers central ; puis on réitère l'opération sur les deux segments restants, et ainsi de suite. On peut voir les six premières itérations du procédé sur le schéma suivant :

Construction
Construction itérative
On dénote par
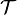
On note A0 = [0,1] et on définit par récurrence une suite de parties de [0,1] par la relation :
On a :
![A_3 = \left[0,\frac{1}{27}\right] \cup \left[\frac{2}{27},\frac{1}{9}\right] \cup \left[\frac{2}{9},\frac{7}{27}\right] \cup \left[\frac{8}{27},\frac{1}{3}\right] \cup \left[\frac{2}{3},\frac{19}{27}\right] \cup \left[\frac{20}{27},\frac{7}{9}\right] \cup \left[\frac{8}{9},\frac{25}{27}\right] \cup \left[\frac{26}{27},1\right].](https://static.techno-science.net/illustration/Definitions/autres/8/83edc64bf4203eea5ddcecde5e52b0d9_94baa2ba7c928782e8650ca6163a5695.png)
Alors l'ensemble de Cantor K3 est « la limite » de An quand n tend vers

Écriture en base 3
On peut aussi définir l'ensemble de Cantor via l'écriture en base 3. Tout réel
![x \in [0,1]](https://static.techno-science.net/illustration/Definitions/autres/c/c628ba2b1047de93f66cb815d986e107_ed07eba36e8ff0203640ec9b2395747a.png)
avec
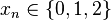
Cette écriture est unique à ceci près : on peut remplacer
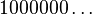
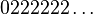
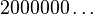
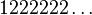
- L'ensemble de Cantor est formé des réels de [0,1] ayant une écriture en base 3 ne contenant que des 0 et des 2.
C'est-à-dire
Note : donc 1/3 est dans cet ensemble, puisqu'il admet les deux écritures 0,1000… et 0,02222… en base 3. 2/3 également (0,2000… ou 0,12222…). Remarquez que parmi les nombres admettant un développement propre et un développement impropre, il n'en existe aucun dont les deux écritures vérifient la propriété demandée.
Variantes

Soit s un nombre strictement compris entre 0 et 1. Si, au lieu de couper chaque intervalle en trois et d'enlever l'intervalle central, on enlève à la n-ème étape un intervalle de longueur s / 3n au centre de chaque intervalle de la génération précédente, on obtient un ensemble de Cantor dont la mesure de Lebesgue est 1 - s. Cela permet d'obtenir un compact d'intérieur vide de mesure aussi proche de 1 que l'on veut. Le cas s = 1 redonne l'ensemble de Cantor usuel. Un procédé comparable est utilisé dans l'ensemble de Smith-Volterra-Cantor.
Une autre version de l'ensemble de Cantor est le carré de Cantor. Il est construit sur le même principe général, mais basé sur un carré : on considère un carré que l'on découpe en 9 carrés de même taille, et on supprime tous les carrés n'étant pas dans un coin du carré de départ. L'ensemble est construit de façon itérative en répétant cette action sur les nouveaux carrés. Ce n'est rien d'autre que le produit cartésien
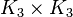
La même construction en dimension 3 conduit au cube de Cantor, égal au produit cartésien
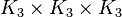
![\mathcal{T} : I \rightarrow I_0 \cup I_1 \ ; \ [a,b] \mapsto \left[a,a+\frac{b-a}{3}\right] \cup \left[b- \frac{b-a}{3},b\right].](https://static.techno-science.net/illustration/Definitions/autres/9/9d2eccc48b7936e07ccd7515045747a0_8d50aa83f8d5a8b19b5cf48cafbf0942.png)
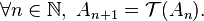
![A_1 = \left[0,\frac{1}{3}\right] \cup \left[\frac{2}{3},1\right];](https://static.techno-science.net/illustration/Definitions/autres/0/0adedfa7e9f4ea3047a129ea092a4fae_2d84b738bd686007460ee4fdacb699a1.png)
![A_2 = \left[0,\frac{1}{9}\right] \cup \left[\frac{2}{9},\frac{1}{3}\right] \cup \left[\frac{2}{3},\frac{7}{9}\right] \cup \left[\frac{8}{9},1\right];](https://static.techno-science.net/illustration/Definitions/autres/b/b7d75520789366adc08dafc57209650a_9cbef45352ad60dd682c629f3d0400ef.png)