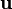Équations fondamentales de la mécanique des milieux continus - Définition

Conditions aux frontières

Afin de pouvoir étudier théoriquement les déformations globales de la Terre (ou d'une planète tellurique), il est nécessaire d'adjoindre aux équations différentielles qui décrivent le mouvement de déformation les conditions qui s'appliquent au centre et sur la surface externe de la Terre, ainsi que des conditions adéquates qui s'appliquent aux diverses frontières internes entre des milieux continus différents. Ainsi, à côté de la continuité du potentiel gravifique et de la force de gravité, il faut tenir compte de deux types généraux de conditions à appliquer lorsqu'on rencontre une interface simple : des conditions cinématiques et des conditions dynamiques.

Conditions cinématiques

Les conditions cinématiques s'obtiennent aisément en exprimant mathématiquement le fait que les points matériels appartenant à une surface-frontière F[x(ξ,t),t] = cste à un instant donné doivent encore appartenir à la même surface à un autre instant, c'est-à-dire σF^{milieu 1} = σF^{milieu 2} ou encore, sous forme eulérienne :

.

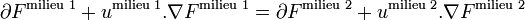
Comme nous nous limitons à des surfaces régulières, la fonction F admet des dérivées partielles continues par rapport au temps et par rapport aux coordonnées spatiales. Il s'ensuit que la composante normale du champ de déplacement relative à l'interface doit être continue, autrement dit

Ces conditions n'excluent pas la possibilité de glissement d'un milieu par rapport à l'autre, et on appellera une frontière sur laquelle un tel glissement est possible une « interface glissante » (en anglais : slip boundary). Par contre, si nous voulons exclure la possibilité de glissement, nous devons imposer la continuité à travers la frontière à la fois des composantes normale et tangentielle du déplacement : u^{milieu 1} = u^{milieu 2}.

Une frontière de ce type est appelée « interface soudée » ou « interface non-glissante » (en anglais : slip-free boundary).

Conditions dynamiques

Pour établir les conditions dynamiques, on considère un petit parallélipipède droit (une « boîte d'allumettes ») de hauteur h. On suppose cette « boîte » partitionnée par une surface-frontière en deux volumes V₁ et V₂ remplis de matériau du milieu continu 1 et de matériau du milieu continu 2, respectivement. La « boîte » est limitée au-dessus par une surface S₁ de normale unitaire extérieure n₁, en dessous par une surface S₂ de normale unitaire extérieure n₂, et sur les côtés par une surface S₃ de normale unitaire extérieure n₃. On applique à ce volume matériel V = V₁ + V₂ limité par la surface fermée S = S₁ + S₂ + S₃ l'équation de conservation de l'impulsion sous forme intégrale, soit

.

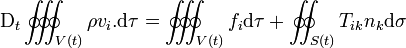
En supposant que les forces volumiques sont continues à travers la frontière, et en laissant tendre h vers zéro, nous obtenons les conditions d'interface dynamiques , en prenant bonne note du fait que pour h = 0, nous avons V = 0, S₃ = 0, et n₁ = − n₂. Ainsi, les composantes normales du tenseur des contraintes dans leur ensemble doivent rester continues au travers l'interface.

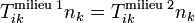
Loi de Hooke

Dans de nombreuses applications géophysiques, particulièrement en sismologie, la Terre est traitée comme un matériau linéairement élastique et isotrope, ce qui signifie que le tenseur lagrangien des tensions élastiques est exprimé par la loi de Hooke. Dans un référentiel cartésien, on a donc

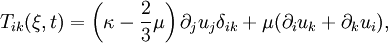
où est le champ des déplacements et où les constantes de matériau κ et μ sont les modules de compression et de cisaillement, respectivement. Dans les problèmes qui concernent des durées s'échelonnant en gros entre une fraction de seconde et quelques heures, c'est-à-dire des laps de temps typiques des périodes des ondes sismiques, des oscillations libres et des marées habituelles, le module de compression à considérer est le module de compression adiabatique, évalué pour des conditions isentropiques. Pour le module de cisaillement, Léon Brillouin a montré en 1940 qu'il n'y avait pas lieu de distinguer entre un cisaillement effectué sous des conditions isentropiques ou des conditions isothermes. D'autre part, on peut tenir compte d'une faible anélasticité en faisant dépendre les coefficients κ et μ de la fréquence ; c'est l'approche adoptée notamment par Kanamori et Anderson et par Dziewonski et Anderson.