Équations fondamentales de la mécanique des milieux continus - Définition

Introduction

Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus, principalement applicables à la déformation des solides et à la mécanique des fluides.

Quelques quantités physiques intégrales du système

En général, on étudie les déformations et la dynamique de la Terre en termes d'un modèle de continuum caractérisé par une distribution interne de masse non spécifiée pour le moment, autrement dit par une densité massique ρ, dans un volume B délimité par une surface . Dans le problème qui nous occupe, cette frontière n'est pas donnée a priori, mais doit être déterminée en supposant qu'elle correspond à la forme d'équilibre du corps déformable. En outre, nous supposerons pour le moment qu'il existe un champ de vitesse v_i par rapport au système de référence choisi mais non encore spécifié, ainsi qu'une densité de moment cinétique interne , une force volumique f_i, un champ de contraintes (ou champ de tensions) T_ij, un moment de force volumique M_i et moment de force surfacique M_ij. Toutes ces quantités peuvent être des fonctions explicites ou implicites du temps t. Sauf indication différente, nous utiliserons un système de référence cartésien dont l'origine (0, 0, 0) se trouve au point O. Nous dénoterons les coordonnées spatiales par x_i et les dérivées spatiales successives , , ... par , , ... (avec i,j = 1,2,3). En règle générale, nous adoptons ici la notation indicielle pour les vecteurs et les tenseurs, ainsi que la règle de sommation d'Einstein sur les indices muets répétés.

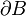
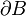
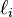
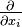
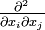
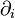
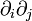
La masse totale du modèle est

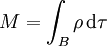
où dτ = dx₁dx₂dx₃ est un élément de volume.

L'impulsion totale est

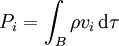
et le moment cinétique total est

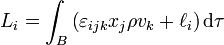
où est le symbole de Levi-Civita.

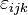
La résultante des forces appliquée au volume B du corps est

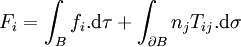
où dσ est un élément de la surface et (n₁,n₂,n₃) dénote un vecteur unitaire normal à la surface et pointant hors du volume B. De la même, manière, le moment de force résultant appliqué au corps B est

.

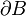
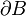
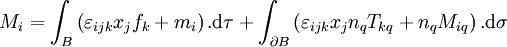
Ces formules sont valables en toute circonstance. Si nous admettons en outre que la surface-frontière de B est régulière et que les champs des tensions et des moments de force surfaciques sont différentiables dans B, on peut appliquer le théorème de la divergence de Gauss et écrire :

.

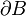
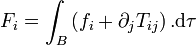
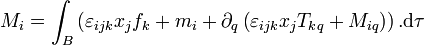
Hypothèses et lois pour décrire les déformations de la Terre

Dans les problèmes de géodynamique théorique, on considère en général que la résultante des forces externes par unité de volume f_i se compose d'une force gravifique volumique causée par l'autogravitation et par l'attraction gravifique de corps extérieurs, d'une force électromagnétique volumique , de forces volumiques inertielles (Coriolis et axifuge) , de forces de marée , et de forces volumiques causées par des charges extérieures . D'autre part, les forces surfaciques T_i(x,t,n) dépendant de l'orientation n qui contribuent en général au tenseur des contraintes T_ij(x,t) via les relations de Cauchy T_i(x,t,n) = T_ij(x,t)n_j(x,t,n) sont les forces élastiques qui engendrent un tenseur des contraintes élastiques , les forces superficielles électromagnétiques qui engendrent un tenseur de Maxwell , des forces visqueuses qui engendrent un tenseur de Reynolds un tenseur des contraintes élastiques , des forces de frottement de contact non visqueux qui engendrent un tenseur des forces de friction un tenseur des contraintes élastiques , et de toute autre force surfacique engendrant un tenseur des contraintes un tenseur des contraintes élastiques .

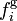
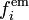
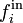
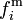
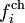
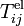
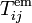
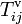
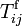
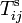
La force de gravité par unité de masse g, plus simplement appelée accélération gravifique ou gravité, dérive d'un potentiel gravifique φ^g que nous assimilerons ici à l'énergie potentielle gravifique :

.

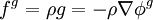
Le potentiel φ^g est déterminé par l'équation de Poisson

,

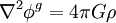
où G est la constante de gravitation. Il convient de noter que les propriétés du potentiel gravifique impliquent que φ^g et g sont des fonctions continues partout dans l'espace, et en particulier sur les frontières entre deux milieux continus différents.

En ce qui concerne le champ de force produit par des interactions électromagnétiques, on admet d'habitude que les points matériels ne transportent pas de charge électrique, c'est-à-dire qu'ils sont électriquement neutres. De la sorte, on suppose qu'aucune force de Lorentz ne s'applique directement à un point massique ξ se mouvant dans le champ magnétique de la Terre. Cependant, le matériau terrestre conduit l'électricité à des degrés divers, autrement dit possède une conductivité électrique σ_e finie non nulle. Dès lors, lorsque ce matériau se déplace à une vitesse v non nulle, il interagit avec le champ géomagnétique interne et engendre une densité de courant électrique induit J qui modifie le champ magnétique initial en donnant naissance à un champ d'induction magnétique variable B(ξ,t) tandis que le flux variable de ce courant produit un champ d'induction électrique E(ξ,t). Le résultat de toutes ces interactions du matériau terrestre en mouvement avec le champ géomagnétique B est la naissance d'un champ de force électromagnétique induit f^em = c ^{− 1}J.B, avec J = σ_e(E + c ^{− 1}v.B), lequel modifie à son tour le mouvement. On a utilisé ici des unités électrostatiques de Gauss, c étant la vitesse de la lumière dans le vide. Il convient de remarquer que dans un diélectrique parfait (σ_e = 0), la force électromagnétique serait nulle (f^em = 0). Sur une interface électromagnétique de normale extérieure n, les quantités n.E,n.H et n.B sont continues. Lorsqu'on étudie les déformations élastiques de la Terre, notamment la propagation des ondes sismiques, les oscillations libres, les déformations de marée, etc., on néglige le plus souvent de considérer de tels phénomènes magnétohydrodynamiques ou magnétoélastiques, en admettant simplement que les forces de rappel élastiques sont beaucoup plus importantes que les forces électromagnétiques. Il faut cependant garder à l'esprit que ces forces existent et sont essentielles lorsqu'on considère la génération du champ géomagnétique interne dans le noyau externe de la Terre par effet de dynamo autoexcitée. Elles peuvent éventuellement devenir importantes lorsqu'on étudie les déformations et oscillations du noyau, mais sont négligeables en pratique lorsqu'on considère des déformations globales de la Terre de faible amplitude.

Les forces d'inertie peuvent se formuler ainsi :

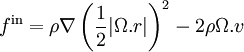
où Ω est le vecteur rotation instantanée, r le vecteur position \mathrm du point matériel \xi, et v la vitesse instantanée de ce point. Le premier terme représente la force axifuge et le second terme représente la force de Coriolis par unité de volume.

Les déformations dues aux marées sont produites par des forces dérivant aussi d'un potentiel, le potentiel de marée W^m. Dans le cas des marées terrestres, compte tenu de la sensibilité des appareils de détection actuellement sur le marché, il est nécessaire de considérer les termes quadrupolaires (n = 2) et termes octupolaires (n = 3) pour la Lune et le Soleil dans le développement général du potentiel de marée en multipôles :

.

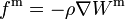
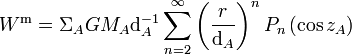
Ici, G dénote la constante de gravitation (G = 6,673.10 ^{− 11}m³s ^{− 2}kg ^{− 1}), M_A est la masse de l'astre générateur de la marée, d_A est la distance du centre de masse de la Terre au centre de masse de A, z_A est la distance zénithale de A et r est la distance du centre de masse de la Terre au point où l'on mesure la marée. Le symbole P_n désigne, comme d'habitude, le polynôme de Legendre de degré n. La première sommation dans l'expression ci-dessus s'étend en théorie sur tous les astres A pouvant engendrer un effet de marée sur la Terre ; en pratique, elle se limite à la Lune, au Soleil et, dans des calculs très précis, à Vénus et Jupiter.