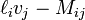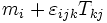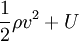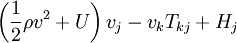Équations fondamentales de la mécanique des milieux continus - Définition
La liste des auteurs de cet article est disponible ici.
Lois de conservation
Les équations régissant un milieu continu peuvent être déduites, soit en utilisant un « principe de correspondance » pour adapter les lois de la mécanique des points discrets de Newton aux points matériels de la mécanique des milieux continus, soit en exprimant de façon directe le fait que certains attributs physiques, tels que la masse, l'impulsion, le moment cinétique, l'énergie cinétique, l'énergie interne, l'énergie totale, etc., contenus dans un volume arbitraire b(t) se déformant au cours du temps t, ne peuvent pas changer de manière arbitraire, mais que leurs changements précis sont régis par des lois de conservation. Ces dernières peuvent s'obtenir en exprimant le taux de changement dans le temps dans un volume arbitraire de matière au moyen du théorème de transport de Reynolds.
Soit b(t) une partie quelconque se déformant au cours du temps du volume matériel B(t). On suppose que sa frontière
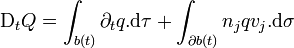
Les notations utilisées ici sont les suivantes :
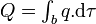
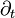
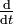
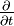
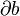
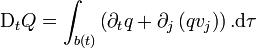
Si κ est le taux local de production ou de destruction de la quantité Q, c'est-à-dire
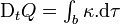
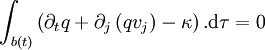
ou, puisque le volume b(t) est arbitraire et peut donc être pris arbitrairement petit :
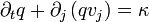
Ceci est la forme eulérienne générale d'une loi de conservation en physique des milieux continus. La forme lagrangienne équivalente, valable pour chaque point matériel individuel, est
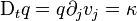
On déduit cette forme lagrangienne aisément de la forme eulérienne à l'aide de l'identité (voir l'article Concepts de base en théorie des milieux continus)
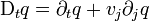
Conservation de la masse, ou équation de continuité
Sous forme intégrale, la conservation de la masse s'exprime par
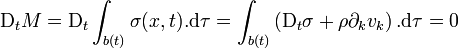
Cette formule fournit l'équation de continuité, exprimant la conservation de la masse sous forme différentielle, en faisant tendre le volume arbitraire b(t) tendre vers un point :
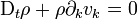
La forme eulérienne de cette dernière équation est
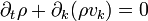
On remarque qu'il s'agit bien ici d'une forme particulière de la loi de conservation générale
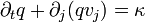
Conservation de l'impulsion, ou équation de mouvement
De manière similaire, à peine plus compliquée, on peut établir l'équation de conservation de l'impulsion régissant le mouvement d'un point matériel, en posant q = ρvi et en admettant explicitement que la masse se conserve aussi. On obtient
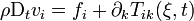
En effet, l'équation fondamentale de la dynamique exprime le fait que le taux de variation de l'impulsion DtPi est équilibré par la résultante des forces Fi agissant sur le volume. On a donc
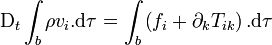
Si nous transformons le membre de gauche au moyen du théorème de Reynolds, nous obtenons
![\mathrm D_t \int_{b(t)} \left[\partial_t \left(\rho v_i \right) + \partial_k \left(\rho v_i v_k \right) \right]. \mathrm d\tau = \int_{b(t)} \left(f_i + \partial_k T_{ik} \right). \mathrm d\tau](https://static.techno-science.net/illustration/Definitions/autres/1/1826f03e31e0f5537164d141acb5ed0e_432cbd69d9b6f135d850cb2d0047c9cd.png)
Dès lors, en faisant tendre le volume arbitraire b vers zéro, on obtient la forme eulérienne générale de l'équation de mouvement, à savoir
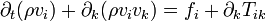
Il convient de noter que dans cette équation, on ne présuppose aucunément qu'il y ait conservation de masse, mais seulement que le tenseur des contraintes Tik est différentiable. En développant le membre de gauche, on obtient
![\rho \left[ \partial_t v_i + v_k \partial_k v_i \right] + v_i \left[ \partial_t \rho + \partial_k \left( \rho v_k \right) \right] = f_i + \partial_k T_{ik}](https://static.techno-science.net/illustration/Definitions/autres/e/ef56caef50481e98526e4199928a8568_367c6c7c34c4bdaff894c0f0f9858ad7.png)
Le terme entre crochets dans le membre de gauche représente l'accélération Dtvi. Le terme entre accolades dans ce même membre de gauche représente simplement l'équation de conservation de la masse sous forme eulérienne. Ainsi donc, si nous supposons que la masse reste conservée — ce qui est pratiquement toujours le cas en géophysique interne — l'équation de conservation de la quantité de mouvement s'écrit
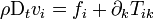
Conservation du moment cinétique, ou équation de rotation
L'équation exprimant la conservation du moment cinétique, qui est primordiale dans les études traitant de la rotation d'un corps déformable comme la Terre, peut être obtenue de manière semblable à celle exprimant la conservation de l'impulsion. En supposant qu'il y ait conservation de la masse et conservation de la quantité de mouvement, on obtient
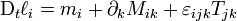
En effet, le taux de variation du moment cinétique DtLi dans un volume arbitraire b est équilibré par le moment de force résultant Mi agissant sur ce volume. Nous avons donc
![\mathrm D_t \int_b \left( \varepsilon_{ijk} x_j \rho v_k + \ell_i \right). \mathrm d\tau = \int_b \left[ \varepsilon_{ijk} x_j f_k + m_i + \partial_q \left( \varepsilon_{ijk} x_j T_{kq} + M_{iq} \right) \right] \mathrm d\tau](https://static.techno-science.net/illustration/Definitions/autres/1/17c090105da76d4f56d1563141cec4e8_0361488fa93d49bd89bbea86b82ee24d.png)
Comme précédemment, on transforme le membre de gauche en appliquant le théorème de Reynolds pour obtenir
![\int_b \left[ \partial_t \left( \varepsilon_{ijk} x_j \rho v_k + \ell_i \right) + \partial_q \left( \rho \varepsilon_{ijk} x_j v_k v_q + \ell_i v_q \right) \right]. \mathrm d\tau = \int_b \left[ \varepsilon_{ijk} x_j f_k + m_i + \partial_q \left( \varepsilon_{ijk} x_j T_{kq} + M_{iq} \right) \right]. \mathrm d\tau](https://static.techno-science.net/illustration/Definitions/autres/e/e1346670572755b8eb16297023587609_ec4da59d0acf632a81b0a52184a19f8d.png)
En faisant tendre le volume arbitraire b vers zéro, on obtient l'équation exprimant localement la conservation du moment cinétique, à savoir
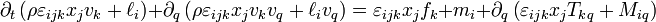
Cette équation peut être réarrangée comme suit :
![\langle\partial_t \ell_i + v_q \partial_q \ell_i\rangle + \varepsilon_{ijk} x_j v_k \left[ \partial_t \rho + \partial_q \left( \rho v_k \right) \right] + \varepsilon_{ijk} x_j \{ \rho \partial_t v_k + \rho v_q \partial_q v_k - f_k - \partial_q T_{kq} \} = m_i + \partial_q M_{iq} + \varepsilon_{ijk} \left( T_{kj}-\rho v_j v_k \right)](https://static.techno-science.net/illustration/Definitions/autres/c/c7f623ecb300ff472ade9b1d50cbebcc_f7f4b3408e372648d8dcc7af06b2c1e9.png)
Dans le membre de gauche, les termes entre chevrons représentent la quantité
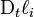
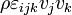
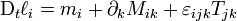
Symétrie du tenseur des contraintes
Si, en outre, nous supposons que le moment cinétique intrinsèque
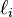
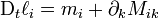
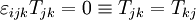
Conservation de l'énergie
L'équation exprimant la conservation de l'énergie peut s'obtenir par la même méthode que celle employée pour la masse, la quantité de mouvement et la quantité de rotation. On trouve :
![\partial_t \left( \rho v^2 + U \right) + \partial_j \left[ \left( \frac{1}{2} \rho v^2 + U \right) v_j - v_k T_{kj} + H_j \right] = v_k f_k + \Gamma](https://static.techno-science.net/illustration/Definitions/autres/7/73a8028b1a4aa40a009ae65649cd2ef0_ce06ba8f2906ee3a932c125bfec2bec3.png)
Le symbole U désigne ici l'énergie interne par unité de volume, Hi est le vecteur densité de flux de chaleur, et Γ est le taux de production ou de destruction intrinsèque d'énergie par unité de volume, par réactions chimiques, par radioactivité, ou par tout autre processus interne. Le symbole v2 représente bien sûr le carré vkvk de la vitesse, c'est-à-dire deux fois l'énergie cinétique par unité de masse.
Tableau récapitulatif des principales lois de conservation
Le tableau ci-dessous résume les principales lois de conservation générales, sous forme eulérienne, utiles pour résoudre les problèmes posés par la mécanique des milieux continus, en particulier lorsqu'il s'agit d'étudier les déformations globales de la Terre suite à un séisme, suite à une variation de la longueur du jour, suite à l'application d'un potentiel de marée ou suite à l'application d'une distribution de masse sur la surface externe. Les notations employées dans le tableau sont celles de ce texte. Rappelons que l'intégrale
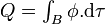
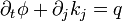
| Q | φ | kj | q |
|---|---|---|---|
| M | ρ | ρvj | 0 |
| Pi | ρvi | ρvivj − Tij | fi |
| Li |
|
|
|
| E |
|
| vkfk + Γ |