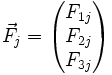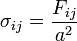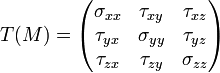Tenseur des contraintes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
sur les tenseurs
Tenseur
Tenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensoriel
Convention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformations
Modules
Algèbre extérieure
Le tenseur des contraintes est une représentation utilisée en mécanique des milieux continus pour représenter l'état de contrainte, c'est-à-dire les forces surfaciques (parfois appelées efforts) mises en jeu entre les portions déformées du milieu. Le terme a été introduit par Cauchy vers 1822.
Comme les forces surfaciques sont définies pour chaque surface coupant le milieu, le tenseur est défini en chaque point du solide, ou localement. L'état de contrainte du solide est donc représenté par un champ de tenseur. On parle aussi de ce fait de champ de contrainte.
Dans le cadre de l'élasticité linéaire, le champ de contrainte est relié au champ de déformation par la loi de Hooke généralisée, c'est-à-dire que l'on peut écrire l'équation tensorielle (et non algébrique) σ = Eε.
Dans le cadre de la géologie structurale et de la tectonique, on parle fréquemment de tenseur de paléo-contraintes. Il représente la partie anisotrope du tenseur des contraintes, responsable des déformations comme les plis, les failles ou les schistosités. La valeur absolue des termes de la matrice n'est pas accessible, mais il est possible de retrouver l'orientation du triaxe principal, ainsi que le rapport d'intensité entre ces trois axes.
Dans certains cas, il est possible de visualiser ces contraintes par la méthode de photoélasticimétrie.
Construction du tenseur
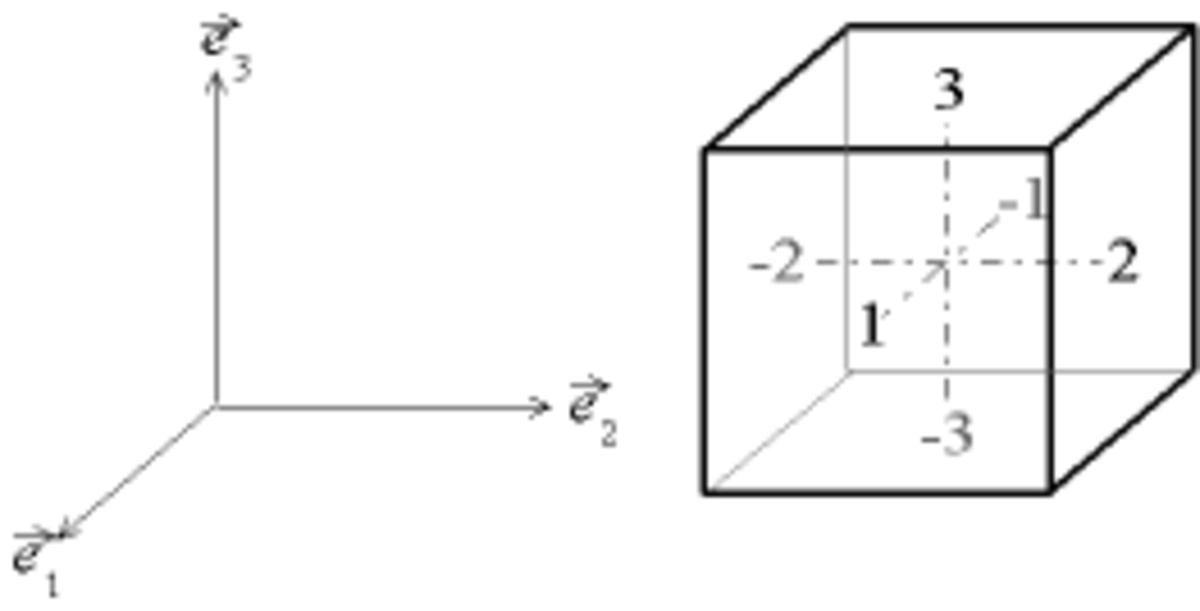
Prenons une base
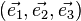
Numérotons ses faces :
- les faces i et -i sont les faces normales à


Dans un premier temps, nous ne considérons que les faces numérotées positivement.
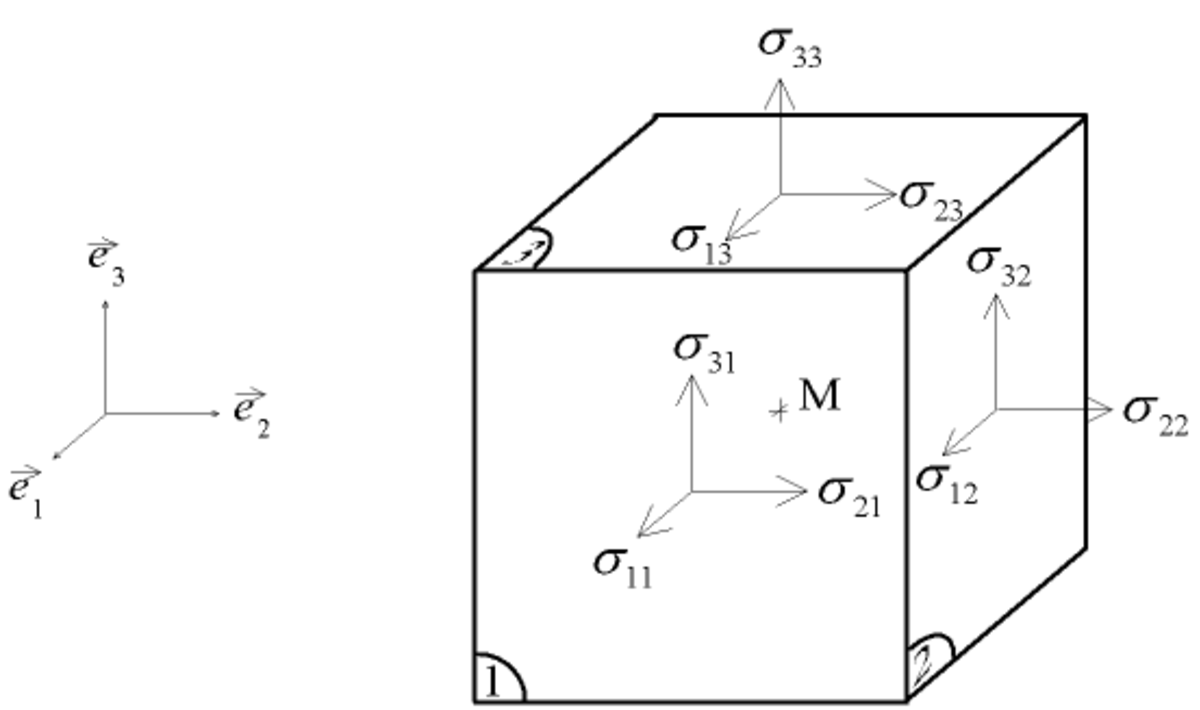
Sur la face j s'exerce un vecteur-force
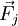
Fij étant la composante selon

On décrit donc l'état de contrainte par le tenseur
T est un tenseur d'ordre 2, à 3 lignes et 3 colonnes. Il est défini localement pour un point M donné.
En mécanique, on n'utilise pas toujours la notation généralisée


Les termes hors diagonale correspondant à du cisaillement, on les note souvent τij , les composantes du tenseur se notent alors :