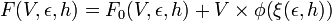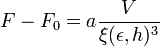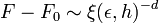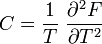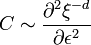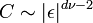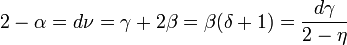Exposant critique - Définition

Relations d'échelle

La théorie d'échelle est une hypothèse supplémentaire très séduisante et bien validée par l'expérience qui consiste à supposer que la seule quantité importante est la longueur de corrélation. La longueur de corrélation ξ dépend bien sûr de ε et de h et, a priori, toutes les fonctions thermodynamiques devraient dépendre de manière compliquée de ces deux variables. L'hypothèse derrière les relations d'échelle est de supposer que la partie «intéressante» des fonctions thermodynamiques (la partie qui décrit les singularités associées à la transition) ne dépend que de ξ et pas directement de ε ou h:

Ici, F est une fonction thermodynamique (typiquement l'énergie libre ou l'enthalpie libre, selon les cas), F₀ est la partie régulière, «inintéressante» de cette fonction et est la partie qui «contient» la transition de phase. On a sorti le volume V en facteur parce que la fonction doit être extensive. Comme ξ est une longueur, la seule formule possible est

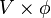
De manière générale, en dimension d

De cette dernière relation, on déduit les relations d'échelle. Par exemple, utilisant la relation thermodynamique

on obtient près du point critique, en oubliant les préfacteurs et les termes réguliers

mais pour h = 0, on a , d'où

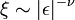
et donc, par comparaison,

α = 2 − dν

Par des raisonnements similaires, on obtient une série d'égalités appelées relations d'échelle

Il y a là quatre égalités pour six inconnues (d est supposé donné). On voit donc qu'il suffit (en général) de connaître deux exposants critiques pour tous les déterminer.

Liste des exposants critiques

Tous les exposants sont définis de manière à être positifs ou nuls.

L'exposant α

La chaleur spécifique diverge au point critique en

(en gardant h = 0)

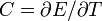
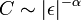
Remarquez que la divergence est présente des deux côtés de la transition.

L'exposant β

Il décrit la manière avec laquelle le paramètre d'ordre dans une petite région tend vers 0 quand la température augmente vers la température critique:

(en gardant h = 0, et seulement pour ε < 0)

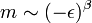
Rappelons que m = 0 pour ε > 0.

L'exposant γ

Il décrit comment la susceptibilité généralisée en champ nul diverge au point critique

(pris en h = 0)

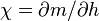
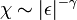
Là encore la divergence est présente que l'on tende de la gauche ou de la droite vers ε = 0. Pour le ferromagnétisme, la susceptibilité généralisée est la vraie susceptibilité, et pour la transition liquide/gaz, il s'agit de qui est, à un facteur près, la compressibilité isotherme.

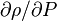
L'exposant δ

Il décrit comment varie le paramètre d'ordre à champ faible quand le système est à la température critique

(en gardant ε = 0)

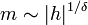
L'exposant ν

Il décrit comment la longueur de corrélation diverge quand on s'approche du point critique

(en gardant h = 0)

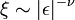
L'exposant η

Juste au point critique, on a et la fonction de corrélation perd sa décroissance exponentielle pour avoir asymptotiquement une décroissance en loi de puissance. L'exposant η caractérise cette loi de puissance

(au point critique, c'est-à-dire ε = 0 et h = 0)

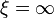
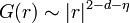
Ici (et dans la suite), d est la dimension du système, c'est-à-dire 3 pour le monde physique.

Notez qu'il n'y a aucune raison a priori de supposer comme on l'a fait que le comportement critique d'une quantité soit le même à gauche ou à droite de T_c; on a utilisé implicitement les résultats de la théorie d'échelle présentée dans la section suivante. Si on décide de ne pas faire cette hypothèse et que l'on veut distinguer l'exposant basse température de l'exposant haute température, on ajoute habituellement un prime aux noms des exposants pour le comportement basse température; par exemple on peut écrire