Exposant critique - Définition

Valeurs des exposants critiques et universalité

Expérimentalement, les exposants critiques ont des valeurs très similaires. Tous les ferromagnétiques semblent avoir des valeurs de β et γ qui vérifient

Les exposants de la transition liquide/gaz ou de la transition superfluide de l'hélium-4 ont des valeurs très proches de celles des ferromagnétiques. On dit que ces exposants sont universels.

La théorie de la renormalisation, développée dans les années 1970 par (entre autres) Kenneth G. Wilson et Leo P. Kadanoff a permis de mieux comprendre l'universalité des exposants critiques et les relations d'échelle. On pense maintenant que les exposants critiques ne dépendent que a) la dimension d du système, b) le caractère courte portée/longue portée des interactions (on ne s'intéresse en fait qu'aux interactions courte portée), c) le nombre de composants n des constituants élémentaires du système (pour un spin quantique, tout se passe comme s'il était orienté selon le champ magnétique et n = 1. Un moment magnétique classique est un vecteur de l'espace et n = 3. Pour un ferromagnétique réel, la valeur de n dépend des symétries du crystal). Il se trouve que les exposants critiques ne dépendent que faiblement de n, ce qui explique la grande homogénéité des valeurs mesurées expérimentalement. Les exposants critiques ne dépendent pas du réseau sous-jacent, du caractère discret ou continu des exposants élémentaires, de la forme précise des interactions (tant qu'elles sont de courte portée).

En dimension d = 1, il n'y a pas de transition de phase.

En dimension d = 2, les exposants critiques sont exactement connus dans le cas n = 1 grâce à la solution du modèle d'Ising en deux dimensions apportée par Lars Onsager en 1944.

En dimension d = 3, on a des mesures expérimentales, des mesures numériques, et des résultats théoriques dues à la renormalisation qui donnent des approximations des exposants. Beaucoup de calculs théoriques sont fait là encore sur le modèle d'Ising.

En dimension , La théorie de Landau (appelée également théorie classique ou théorie de champ moyen) prédit des valeurs pour les exposants critiques. (Historiquement, ce fut une surprise que la théorie de Landau ne s'applique pas aux systèmes réels en d = 3.)

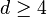
Voici les valeurs tirées du livre de Kadanoff:

Valeurs des exposants critiques

	α	β	γ	δ	ν	η
Ising d = 2	0	1/8	7/4	15	1	1/8
Ising d = 3	0,104	0,325	1,23	5,2	0,632	0,039
Théorie de Landau	0	1/2	1	3	1/2	0