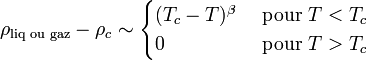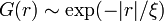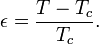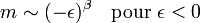Exposant critique - Définition

Introduction

Lors d'une transition de phase de deuxième ordre, au voisinage du point critique, les systèmes physiques ont des comportements universels en lois de puissances caractérisées par des exposants critiques.

Paramètre d'ordre et point critique

Premier exemple

Au point critique, un fluide est caractérisé par une température critique T_c et une densité critique ρ_c. Pour une température T légèrement supérieure à T_c (à nombre de particules et volume constants), le système est homogène avec une densité ρ = ρ_c. Pour une température légèrement inférieure à T_c, il y a une séparation de phase entre une phase liquide (de densité ρ_liq > ρ_c) et une phase gazeuse (de densité ρ_gaz < ρ_c). On observe que

où est l'un des exposants critiques associés à ce problème.

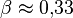
Ici, la notation est un log-équivalent, ce qui signifie que log | ρ_{liq ou gaz} − ρ_c | est l'équivalent mathématique de log[(T_c − T)^β] quand T tend vers T_c par le bas. Cela signifie qu'il y a un préfacteur dans la formule ci-dessus (positif pour le liquide, négatif pour le gaz) et peut-être même des corrections logarithmiques. On ne s'intéresse cependant qu'à l'exposant critique β et non au préfacteur pour une raison très simple: l'exposant est universel et ne dépend pas du corps pur choisi pour réaliser l'expérience (alors que le préfacteur ou la température critique T_c en dépendent).

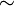
Deuxième exemple

Un ferromagnétique est un corps qui conserve une aimantation spontanée en l'absence de champ magnétique extérieur. On observe cependant que si on le chauffe, ce corps perd son aimantation assez brutalement à une certaine température T_c dite température critique ou température de Curie. Si on mesure la magnétisation m d'une petite région du système, on observe que

où β est encore l'un des exposants critiques associés à ce problème. La valeur de β pour le ferromagnétisme est très proche, et sans doute identique (voir plus bas), à celle de la transition liquide/gaz.

Formulation générale

On considère une transition de phase de second ordre (sans chaleur latente) à une température critique T_c. La transition est caractérisée par un paramètre d'ordre, noté m, qui est uniforme et nul pour T > T_c, mais non-nul et non-uniforme (à l'échelle du système) pour T < T_c: quand on est en dessous de T_c, le système se sépare en plusieurs régions ou phases telles que le paramètre d'ordre prend des valeurs différentes entre deux régions, mais reste uniforme à l'intérieur d'une région donnée.

Pour la transition liquide/vapeur, le paramètre d'ordre est ρ − ρ_c et le système se décompose en deux phases en dessous de la température critique (liquide et gaz). Pour le ferromagnétisme, le paramètre d'ordre est la magnétisation et le système se découpe en de nombreuses régions de magnétisation uniforme qui sont les domaines de Weiss. Pour la transition superfluide de l'hélium-4 ou la transition supraconductrice, le paramètre d'ordre est la fonction d'onde du condensat.

Le paramètre d'ordre peut être un réel (liquide/gaz), un vecteur (ferromagnétisme), un nombre complexe (superfluidité et supraconductivité).

Au paramètre d'ordre est associé un champ conjugué (au sens thermodynamique), noté de manière générique h qui est la quantité qu'un expérimentateur manipulerait pour fixer la valeur du paramètre d'ordre. Pour le ferromagnétisme, le champ conjugué est le champ magnétique B. Pour la transition liquide/gaz, c'est P − P_c, où P est la pression et P_c la pression au point critique (on s'arrange toujours pour que le champ conjugué s'annule au point critique).

Une quantité très importante dans ces phénomènes est la longueur de corrélation ξ, qui décrit la taille d'une fluctuation du paramètre d'ordre ou, de manière équivalente, la distance qu'il faut parcourir pour que le paramètre d'ordre puisse changer de manière significative. Mathématiquement, on définit une fonction de corrélation (où m(r) est la valeur de m à la position r, et où signifie une moyenne sur toutes les réalisations du systèmes). On observe que G(r) décroît exponentiellement avec la distance, et le taux de décroissance est donné par la longueur de corrélation:

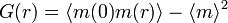
La longueur de corrélation diverge au point critique.

Pour simplifier les notations, on définit une température réduite ε par

On est donc dans la région haute température (paramètre d'ordre uniforme et nul) pour ε > 0 et dans la région basse température (paramètre d'ordre non-nul et non-uniforme) pour ε < 0. La théorie des phénomènes critiques fournit des prédictions pour .

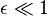
On définit enfin des exposants critiques, tel β par des relations du genre