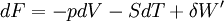Énergie libre - Définition

En thermodynamique l’énergie libre F (appelée aussi "énergie libre de Helmholtz") est une fonction d’état extensive dont la variation permet d'obtenir le travail utile susceptible d'être fourni par un système thermodynamique fermé, à température constante. Elle correspond à l'énergie libre de Helmholtz des anglo-saxons, qui préférent la symboliser par la lettre A.

À ne pas confondre avec la fonction enthalpie libre G ("énergie libre de Gibbs" des anglo-saxons), qui s’applique aux systèmes évoluant à la température T et à pression constante (cas des réactions effectuées à l’air libre).

L'énergie libre est souvent utilisée dans l'étude des explosions qui induisent une variation de pression ou encore dans la calorimétrie à volume constant effectuée dans une bombe calorimétrique.

Néanmoins le rôle de la fonction F est beaucoup moins important en thermochimie que celui de la fonction enthalpie libre qui est la fonction phare, indispensable à l’étude des équilibres chimiques.

Définition

Considérons une transformation irréversible effectuée à la température T et à volume constant. S’il n’y a pas de montage électrochimique, il n’y a pas de travail électrique. Comme V=cte, le travail des forces de pression est nul.

Donc en appliquant le premier principe :

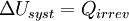
Appliquons alors le second principe : 0~" >

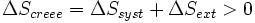
Le système échange avec le milieu extérieur Q_irrév. Si on se place du côté du milieu extérieur, celui-ci reçoit - Q(irrév) = - ΔU(syst).

Et la variation d’entropie du milieu extérieur devient égale à :

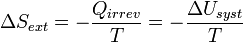
D’où : 0~" >

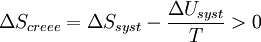
Multiplions par ( - T )

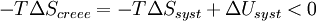
On définit ainsi la fonction énergie libre :

Pour une transformation effectuée à T et V = cte, on obtient :

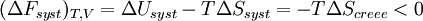
Si la transformation est réversible, et

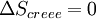
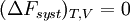
En revanche, si la transformation est irréversible, 0~" > et donc

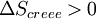
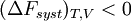
La transformation réelle à T et V = cte, ne peut s’effectuer qu’avec une diminution de l’énergie libre du système.

Différentielle de F

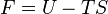
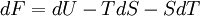
• Appliquons le premier principe

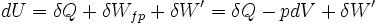
avec:

δW_fp : travail des forces de pression

δW': travail autre, comme par exemple le travail électrique dans un montage de pile

• Appliquons le second principe

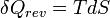
dU s'exprime donc:

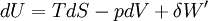
d'où :

• Si la température est constante:

'

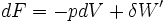
• Cas d'une transformation réelle donc irréversible

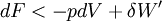
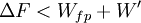
On montre bien que la variation de la fonction F est égale au travail fourni par le système si la transformation est réversible et est effectuée à T constante .

• Si le volume est constant et le travail W' est nul:

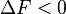
plus précisément :

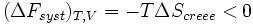
La transformation réelle à T et V = cte, ne peut s’effectuer qu’avec une diminution de l’énergie libre du système. On peut donc identifier F au potentiel thermodynamique d'une transformation isotherme et isochore

Relations utiles à partir de F ou de ses différentielles

• Relation de maxwell :

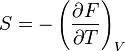
• Relation de Gibbs-Helmholtz : il existe une relation analogue à celle de Gibbs-Helmholtz concernant F :

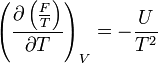
• Potentiel chimique : une "définition" du potentiel chimique peut être donnée à partir d'une différentielle partielle de F.

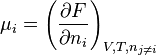
Autres fonctions d'état

• Énergie interne
• Enthalpie
• Enthalpie libre
• Entropie
• Température
• Volume
• Pression

Réferences

• IUPAC definition
• Atkins' Physical Chemistry, 7th edition, by Peter Atkins and Julio de Paula, Oxford University Press
• Landau, L. D.; Lifshitz, E. M. (1986). Theory of Elasticity (Course of Theoretical Physics Volume 7), (Translated from Russian by J.B. Sykes and W.H. Reid), Third ed., Boston, MA: Butterworth Heinemann. ISBN 0-7506-2633-X.