Glossaire de topologie - Définition

Propriétés d'espaces topologiques

Les espaces topologiques peuvent être qualifiés de différentes manières en termes de , de ou de .

Axiomes de séparation

Certains des termes employés ici peuvent avoir été définis autrement dans la littérature ancienne (voir l'histoire des axiomes de séparation).

T₀ ou de Kolmogorov : dans lequel pour tout couple de points distincts, il existe un voisinage de l'un qui ne contient pas l'autre.

T₁ ou accessible ou de Fréchet : dont tous les singletons sont fermés.

T₂ ou de Hausdorff ou séparé : dans lequel deux points distincts admettent toujours des voisinages disjoints.

T_2½ ou complètement de Hausdorff : dans lequel deux points distincts admettent toujours des voisinage fermés disjoints.

Régulier : séparé et dont tout point admet une base de voisinages fermés.

Complètement régulier ou de Tychonoff : séparé et uniformisable, ou encore : sous-espace d'un compact.

Faiblement normal : complètement régulier et dans lequel deux ouverts disjoints quelconques ont deux voisinages fermés disjoints dont l'un est à .

Normal : séparé et dans lequel deux fermés disjoints quelconques possèdent toujours des voisinages disjoints. Le lemme d'Urysohn garantit alors que ces deux fermés sont .

Complètement normal : dont tout sous-espace est normal.

Parfaitement normal : séparé et dont tout fermé est le lieu d'annulation d'une fonction continue réelle.

Axiomes de recouvrement

Les axiomes de recouvrement traitent de l'existence de ou de particuliers pour un quelconque de l'espace considéré.

Paracompact : espace séparé dont tout recouvrement ouvert admet un raffinement localement fini.

Lindelöf : dont tout recouvrement ouvert admet un sous-recouvrement dénombrable.

Quasi-compact : dont tout recouvrement ouvert admet un sous-recouvrement fini.

Compact : quasi-compact et .

Le terme compact est utilisé en anglais pour décrire un quasi-compact. Le risque de confusion peut alors amener à préciser « compact Hausdorff » pour désigner l'acception française.

Voir aussi .

σ-compact ou sigma-compact : recouvert par une famille dénombrable de parties compactes.

Localement compact : séparé, et dont chaque point admet un compacts.

Séquentiellement compact : dans lequel toute suite admet au moins une .

Connexité

Les hypothèses de connexité décrivent la cohésion de l'espace ou de certains voisinages, ou l'existence de déformations () entre certaines applications vers l'espace considéré.

Connexe : qui n'est pas l'union disjointe de deux ouverts non vides.

Voir aussi .

Localement connexe : dont chaque point admet un connexes.

Totalement discontinu : dont les seules parties connexes sont les singletons.

Connexe par arcs : dont tout couple de points (x,y) est relié par un chemin (ou arc), c'est-à-dire une application continue telle que p(0) = x et p(1) = y.

Un espace connexe par arcs est connexe.

Localement connexe par arcs : dont chaque point admet un connexes par arcs.

Un espace localement connexe par arcs est connexe si et seulement s’il est connexe par arcs.

Simplement connexe : connexe par arcs et dans lequel toute application continue est homotope à une application constante.

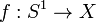
Contractile : pour lequel l'application identité de X est homotope à une application constante.

Les espaces contractiles sont toujours simplement connexes.