Graphe planaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans la théorie des graphes, un graphe planaire est un graphe qui a la particularité de pouvoir se représenter sur un plan sans qu'aucune arête (ou arc pour un graphe orienté) n'en croise une autre. Autrement dit, ces graphes sont précisément ceux que l'on peut plonger dans le plan.
Les méthodes associées à ces graphes permettent de résoudre des problèmes comme l'énigme des trois maisons et d'autres plus difficiles comme le théorème des quatre couleurs.
Exemples et contre-exemples
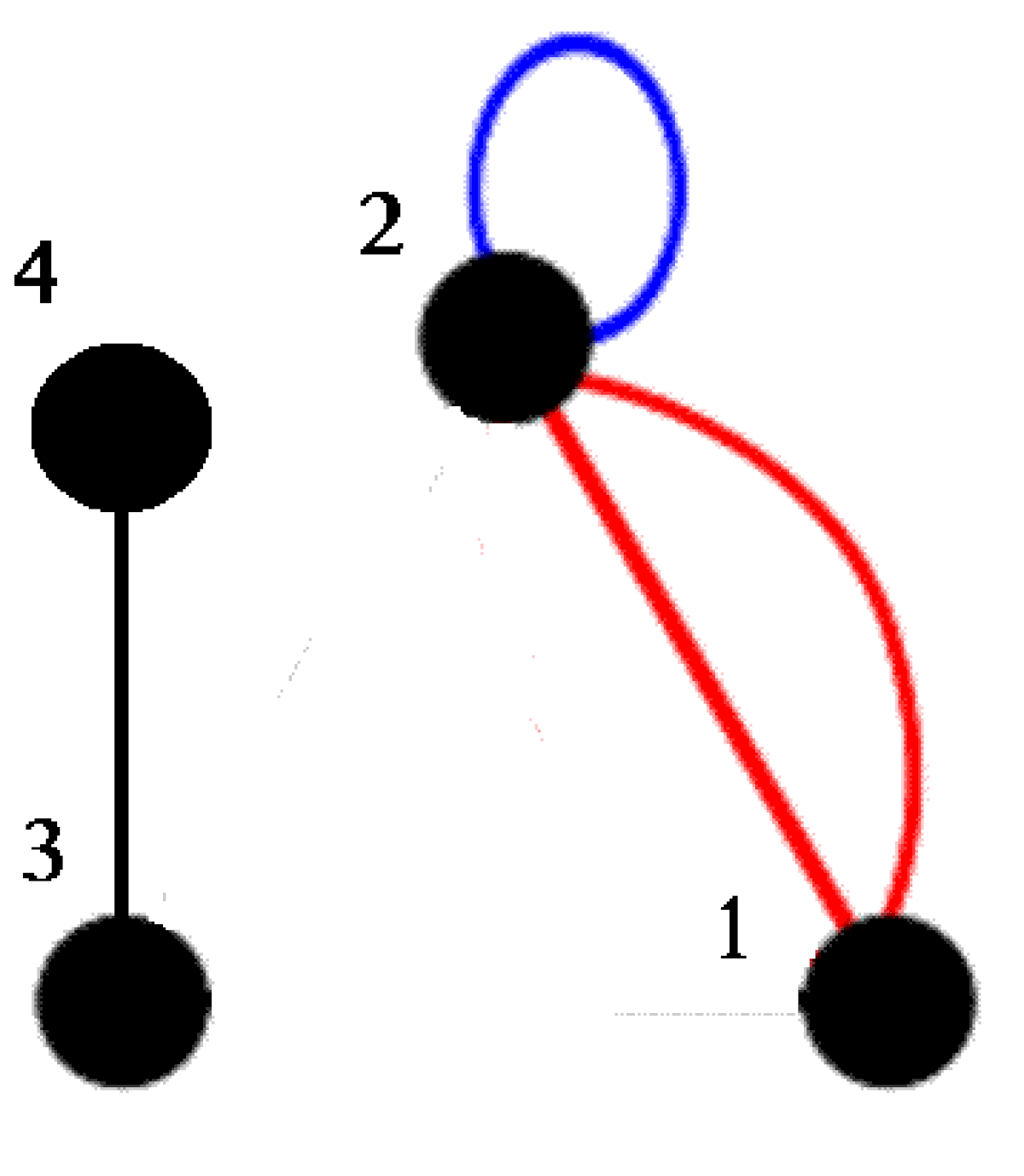
1) 2) 3) 4)
- Ce graphe est clairement planaire, car il n'existe pas d'intersection entre deux arêtes.
- C'est un graphe complet à quatre sommets (K). Il est planaire : si on déplace le sommet 4 dans le triangle 1 2 3, on constate qu'il n'y a plus d'intersection d'arêtes.
- C'est un graphe complet à 5 sommets (K). Il n'est pas planaire.
- C'est un graphe biparti complet à 6 sommets, 3 d'entre eux se connectant aux trois autres (K). Il n'est pas planaire.
En fait, K et K sont les plus petits graphes non planaires, ce qui découle de la caractérisation ci-dessous.
Propriétés
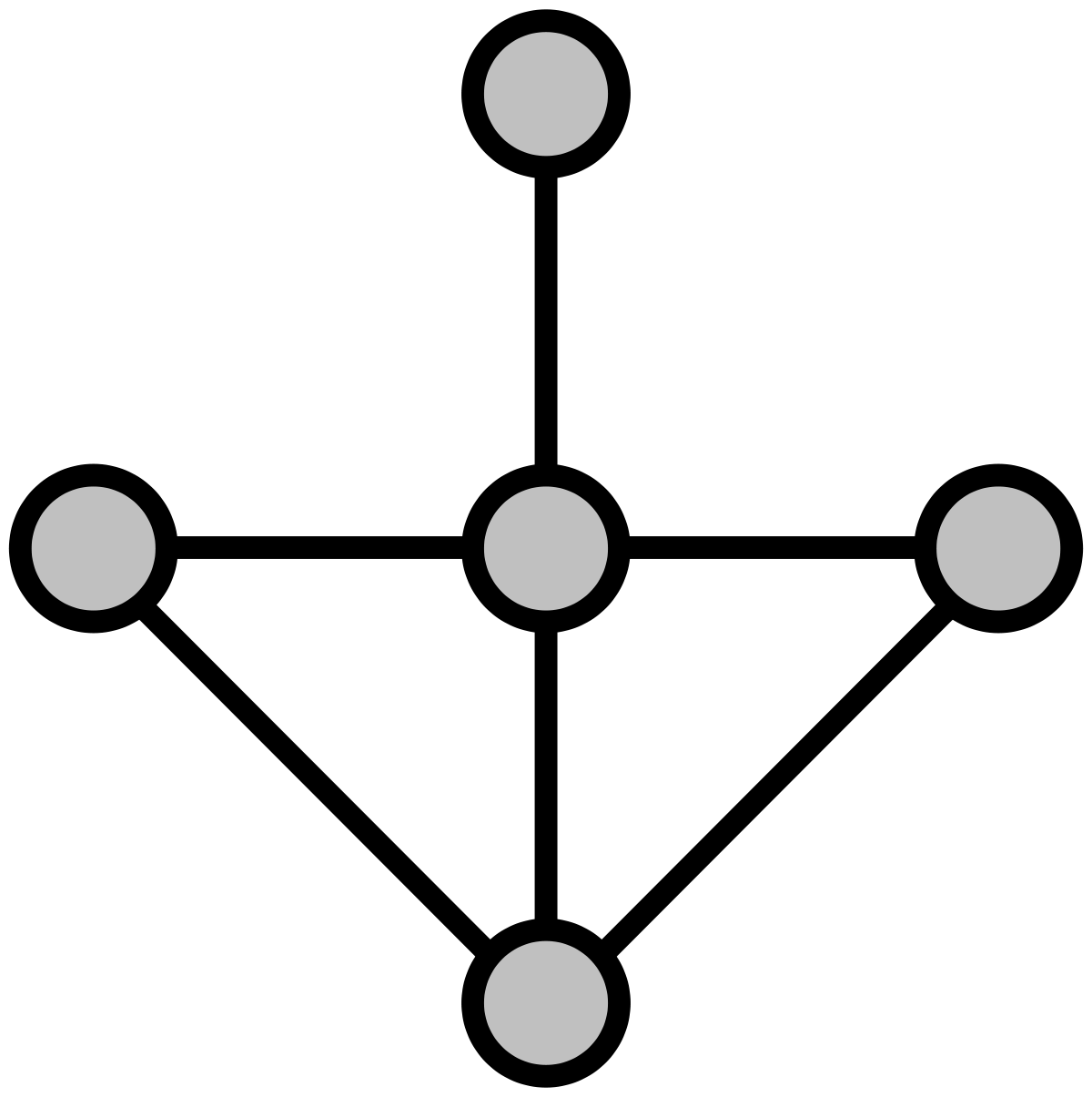
Dans toute la suite du paragraphe, G désigne un graphe planaire, n son nombre nœuds, a son nombre d'arêtes (ou de liens) et f son nombre de face. Une face est une composante connexe du complémentaire du graphe dans le plan. Le degré d'une face F est la longueur de son cycle frontière, on considère un chemin le plus court possible d'origine confondue avec son extrémité, le nombre d'arêtes (avec leur multiplicité) est le degré de la face F. Il est noté deg (F). On obtient une première formule presque évidente :
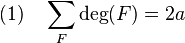
En effet, chaque arête élément d'un cycle borde deux faces, une arête partagée par aucun cycle est parcourue deux fois par le chemin frontière de la composante non bornée du complémentaire du graphe.
La formule d'Euler, pour un graphe planaire connexe est la suivante :

Une méthode simple pour la démontrer est de l'établir pour un graphe sans cycle (à une face), puis par récurrence d'ajouter les arêtes qui engendrent des cycles. Cette formule permet de démontrer que tout graphe simple planaire connexe, ayant au moins trois sommets, vérifie la majoration suivante.
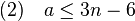
Un graphe simple est un graphe sans boucle (une boucle est une arête qui possède une origine et une extrémité confondues) et sans arête multiple (des arêtes multiples sont des arêtes ayant même origine et même extrémité). Cette formule se démontre simplement, toute face dispose d'un degré au moins égal à 3, car le graphe comporte au moins trois nœuds et est simple. On en déduit de la formule (1), que 3.f est inférieur ou égal à 2.a. La formule d'Euler permet de conclure.
Cette majoration est à l'origine d'une démonstration du fait que K5 n'est pas planaire. En effet, K5 dispose de 10 arêtes, et 5 nœuds, ce résultat est incompatible avec la majoration (2). Si, avec les hypothèses de la majoration (2), le graphe est sans triangle, on dispose alors de la majoration :

Le raisonnement est le même, mais cette fois-ci le degré d'une face est au moins égal à 4. On en déduit que K3,3 n'est pas planaire. Les détails sont donnés dans l'article Énigme des trois maisons.
Un premier lemme est utile :
-
- Tout graphe planaire connexe peut s'obtenir en adjoignant des arêtes à un arbre connexe ayant les mêmes nœuds :
Un arbre est un graphe ne contenant qu'une unique face. On procède par récurrence f le nombre de faces du graphe.
Supposons que le graphe ne possède qu'une unique face, le graphe est un arbre et la proposition est trivialement vérifiée. Supposons que la proposition vraie pour f et montrons là pour un graphe G à f + 1 faces. Le théorème de Jordan montre que s'il existe plusieurs faces, il existe une courbe de Jordan formée par des arêtes. Si l'on retranche une des arêtes A de la courbe au graphe G, les parties droite et gauche du complémentaire du graphe, qui formaient précédemment deux faces, n'en font plus qu'une et ce qui reste de la courbe de Jordan garantit que G est toujours connexe. Le graphe amputé de A vérifie les hypothèses de récurrence et s'obtient en adjoignant des arêtes à un arbre connexe. Ajouter la dernière arête A fournit le graphe initial.
-
- Formule d'Euler :
Démontrons la proposition tout d'abord pour un arbre, par récurrence sur n son nombre de nœuds. Si l'arbre ne contient qu'un unique nœud, il possède une face et aucune arête, la formule est vérifiée. On suppose que la formule est vraie pour n, montrons là pour un arbre G contenant n + 1 nœuds. Comme l'arbre ne contient qu'une unique face, il contient au moins un nœud N connecté à une unique arête (sinon le théorème de Jordan garantirait l'existence d'au moins deux faces.). L'arbre G ôté de ce nœud et de l'arête adjacente est un arbre connexe contenant n nœuds, il vérifie l'hypothèse de récurrence. Ajouter le nœud N et l'arête associé, correspond à ajouter un nœud et une arête, la formule d'Euler reste vraie pour G, ce qui termine cette première étape.
Démontrons maintenant la proposition pour un graphe connexe par récurrence sur f son nombre de faces. Si f est égal à 1, la formule est vérifiée d'après la récurrence précédente. Supposons la vraie pour tout arbre ayant f faces et montrons là pour un graphe G ayant f + 1 faces. La récurrence du lemme montre qu'il est possible de retrancher une arête à G de telle manière à ce que le nouveau graphe soit encore connexe et ait exactement f faces. La formule d'Euler est alors vérifiée par hypothèse de récurrence. Rajouter l'arête manquante ne modifie pas le nombre de nœuds, et incrémente de un le nombre d'arêtes et de faces. La formule d'Euler est encore vérifiée, ce qui termine la démonstration.