Groupe des unités d'un anneau d'entiers quadratiques - Définition

Fraction continue

Cette question date du III^e siècle, sous une forme un peu différente. L'équation de Pell-Fermat, sous une forme un peu réduite, est l'équation diophantienne suivante :

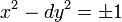
Ici, d désigne un entier strictement positif non carré parfait. Les mathématiciens indiens du VI^e siècle aussi ainsi que les européens du XVII^e siècle. Les indiens ainsi que les européens ont chacun développé une méthode de résolution efficaces.

Généralités

L'objectif est de trouver l'unité fondamentale ρ présente dans le premier quadrant. Si les deux entiers a et b sont définis par ρ = a + b.ω, selon la configuration de ω, cela revient à trouver un couple de solution (a, b) d'une des deux équations suivantes avec a et b choisi positifs, différent du couple (1,0) et a de valeur la plus petite possible :

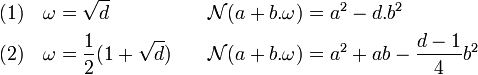
Placons nous dans le cas (1). Soit h / k une fraction formé de deux entiers strictement positif, tel que h soit différent de 1, tel que (h, k) soit solution de l'équation (1). Alors la fraction h / k approche bien ω au sens où la valeur absolue de leur différence est plus petite que l'inverse de 2.k². Ceci garantit que h / k est une réduite de la fraction continue de ω. Comme ω est un nombre quadratique, sa fraction continue est périodique à partir d'un certain rang. Les solutions de l'équation (1) se correspondent aux réduites en avant dernière position dans la période. Comme les différentes réduites possèdent des numérateurs et dénominateurs strictement croissants, l'unité fondamentale correspond à la réduite de la première période.

Dans le cas où ω est de type (2), les résultats précédents sont toujours valables, mais c'est la fraction continue de -ω_c qui est concernée.

Joseph-Louis Lagrange étudie théoriquement l'équation (1). Il montre qu'elle possède une infinité de solutions, que ces solutions se trouvent toutes (au signe près) dans la fraction continue de ω, qu'on en trouve exactement une par période et que sa position correspond à l'avant-dernière. Ces éléments permettent aisément de démontrer le théorème structurel pour les anneaux d'entiers quadratiques. Les raisonnements s'appliquant de la même manière pour l'équation (2).

Illustration par l'exemple

Supposons que ω soit égal à 1/2(1 + √61). On remarque que 61 est un congru à 1 modulo 4. Calculons la fraction continue de -ω_c :

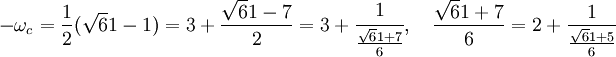
On continue avec le même algorithme :

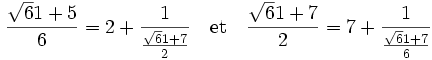
Le dernier quotient complet est égal au premier, la suite de la fraction est une répétition et l'on possède une période complète. On en déduit la fraction continue, ainsi que l'expression des réduites, notées ici h_i / k_i :

L'indice correspondant à l'avant dernière période est le 2, on en déduit que a = 17 et b = 5. On vérifie l'égalité dans l'équation (2). On remarque de 1/4(d-1) est égal à 15 et :

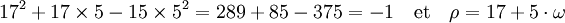
Méthode chakravala

La méthode indienne est un peu équivalente à celle des fractions continues. La seule différence dans l'algorithme réside dans le fait que les coefficients de la fraction continue ne sont pas nécessairement positifs. La convention utilisée consiste à choisir le coefficient tel que le quotient complet soit, en valeur absolue le plus grand possible. Elle accélère de fait un peu l'algorithme.

Elle utilise un accélérateur décrit et démontré par Wallis qui s'applique aussi pour les fractions continues. Si l'on dispose un entier quadratique α de norme, en valeur absolue égale à 2, alors 1/2α² est une unité et si l'on dispose d'un entier quadratique de norme, en valeur absolue égal à 4, alors le huitième de son cube est une unité.

La logique est ici algébrique et non analytique comme chez Lagrange, les démonstrations théoriques associées à l'explicitation de la structure du groupe des unités sont en conséquence plus proches de cet article que des fractions continues. Elles se trouvent dans l'article détaillé. À l'époque de la mise au point de la méthode, les mathématiciens indiens ne se préoccupaient pas de question de cette nature. Les preuves sont la conséquence d'un regard moderne sur leur travail.