Méthode chakravala - Définition

Introduction

En mathématiques et plus précisément en arithmétique, la méthode chakravala est un algorithme pour résoudre les équations diophantiennes équivalentes à celles de Pell-Fermat. Une équation diophantienne est une équation à coefficients choisis dans les nombres entiers et les solutions recherchées sont entières. L'équation traitée est équivalente à :

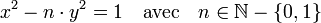
Cette méthode fut développée en Inde et ses racines peuvent être retracées jusqu'au V^e siècle. Initié par Aryabhata, elle est développée plus avant par Brahmagupta et Bhaskara II.

Selenius, pour son évaluation de la méthode chakravala, énonce : «  La méthode représente un algorithme de meilleure approximation de longueur minimale qui, en raison de plusieurs propriétés de minimisation, avec un effort minimal et évitant les grands nombres produit automatiquement les meilleures solutions de l'équation. La méthode chakravala anticipa les méthodes européennes de plus d'un milliers d'années. Mais aucune performance européenne dans le champ entier de l'algèbre beaucoup plus tard après Bhaskara, n'égala la complexité merveilleuse et ingénieuse de chakravala. »

Il faut en effet attendre de XVII^e siècle pour que l'Europe redécouvre de manière indépendante les résultats des travaux des mathématiciens indiens.

Objectif

Une forme d'équation de Pell-Fermat s'exprime de la manière suivante :

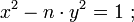
Ici n désigne un entier strictement plus grand que 1 et sans facteur carré, ce qui signifie que le seul carré parfait qui divise n est égal à un. L'équation est diophantienne ce qui signifie que les couples (x₀, y₀) recherchée sont des couples de nombres entiers. Toutes les solutions s'expriment à partir du couple solution formée de deux entiers minimaux en valeur absolue dans l'ensemble des solutions. La méthode chakravala permet d'obtenir un couple de cette nature.

L'égalité suivante est un exemple de solution, elle est connue des indiens depuis avant notre ère :

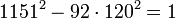
Apports de Brahmagupta

Décors

Les méthodes proposées ici utilisent la puissance du formalisme actuel. Si le contenu mathématique est analogue à celui de Brahmagupta, les techniques d'exposition ainsi que les démonstrations ne reflètent pas la pensée du mathématicien indien. Les notations suivantes sont utilisées dans tout le reste de l'article. On considère l'équation diophantienne suivante, où n est un entier plus grand que 1 et sans facteur carré :

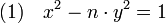
Soient A l'anneau des nombres irrationnels de la forme a + √n.b, où a et b désignent deux nombres entiers. Soient N l'application qui au nombre a + √n.b associe a² - n.b² et φ l'application qui à a + √n.b associe φ(a + √n.b) = a - √n.b.

La fonction N correspond à la norme de A au sens de la théorie algébrique des nombres. Elle possède une propriété bien utile. Un nombre α de A égal à a +√n.b correspond à une solution (a, b) de l'équation (1) si et seulement si N(α) est égale à 1. Ainsi, l'équation (1) peut encore s'écrire N(ξ ) = 1. Pour cette raison si α est un élément de A vérifiant N(α) = 1, on dit que α est racine de l'équation (1).

La fonction φ possède aussi d'utiles propriétés. C'est un automorphisme de A :

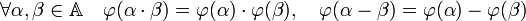
L'application φ est involutive c'est-à-dire que composée deux fois de suite avec elle-même, elle est égale à l'identité, ou encore son application inverse est égale à elle-même :

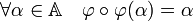
Enfin, l'application φ offre une expression de la norme :

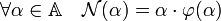
Si l'on note α = a + √n.b, elle provient du calcul suivant :

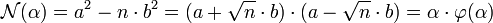
Samasa

La première propriété utilisée est la suivante :

• Soit α et β deux éléments de A, alors :

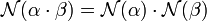
Si α = a₁ + √n.a₂ et β = b₁ + √n.b₂ cette égalité s'écrit :

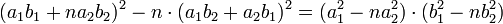
Cette égalité est connue sous le nom de Identité de Brahmagupta que les indiens l'appelaient Samasa. Pour se convaincre de son exactitude, il suffit d'exprimer N en fonction de l'automorphisme φ :

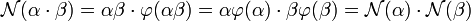
Un cas particulier correspond à celui où β est un entier k, l'égalité prend la forme suivante :

• Soit α un élément de A et k un entier, alors :

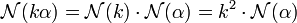
Conséquences

• Soit α un élément de A tel que N(α) = 1, alors α ^-1 est un élément de A et il vérifie N(α ^-1) = 1 et α ^-1 = φ(α).

En effet, dire que N(α) = 1, c'est dire que α.φ(α) = 1, ce qui montre que φ(α) est l'inverse de α et en appliquant φ à l'égalité α.φ(α) = 1, on obtient en remplaçant φ(α) par α ^-1 : α ^-1.φ(α ^-1) = 1

• Si l'équation (1) admet une solution différente de +/- 1, alors elle admet une infinité de solutions distinctes.

En effet, si α est une solution, α ^-1 en est une aussi, d'après la proposition précédente et comme la norme d'un produit est égal au produit des normes, on dispose des égalités suivante :

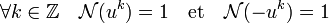
Il suffit de démontrer que les puissances de α sont toutes distinctes. Cette réalité provient du fait que si un nombre réel x vérifie x^k = 1, où k est un entier différent de 0, alors x est égal à +/- 1. Soit k et l deux entiers tel que α^k = α^l alors α^k-l est égal à 1 et comme α est différent de 1 et -1, k - l est égal à 0.

Comprendre comment fait Brahmagupta pour résoudre l'équation (1) dépend de trois propositions, maintenant simples à démonter :

• Soit α un élément de A tel que N(α) = -1, α ² est solution de (1).

Il suffit de remarquer que la norme de α ² est le carré de la norme de α et est égal à 1.

• Soit α un élément de A tel que N(α) soit égal à +/- 2, alors 1/2.α² est un élément de A solution de (1).

En effet, si α est égal à a + b.√n alors un calcul montre que α² = a² + n.b² + 2ab.√n. Comme a² + n.b² = N(α) + 2.n.b² et que N(α) et 2ab sont des multiples de 2, α² l'est aussi. Le calcul suivant permet de conclure :

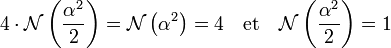
• Soit α un élément de A tel que N(α) soit égal à +/- 4 et tel que 2 ne divise pas α, alors 1/8.α³ est un élément de A de norme égale à +/- 1.

En effet, calculons α³ :

En remarquant que N(α) = a ² - n.b ² = +/- 4, on obtient :

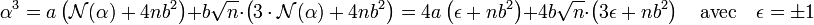
Comme ε est impair, il suffit de montrer que b est impair pour prouver que α³ est un multiple de 8. Si b est pair, n.b ² est un multiple de quatre et comme N(α) = a ² - n.b ² est aussi un multiple de quatre, a est pair. Or par hypothèse α n'est pas un multiple de deux et a et b ne peuvent être pairs simultanément. En conséquence, b est impair et ε + nb² ainsi que 3ε + nb² sont pairs si n est impair. Ceci montre que α³ est bien un multiple de 8 si n est impair.

Or n est toujours impair. En effet, si n est pair, comme N(α) est pair, a l'est aussi et a ² est un multiple de quatre, donc comme n n'a pas de facteur carré, n n'est pas un multiple de quatre donc b est pair et α est un multiple de 2, ce qui est contraire à l'hypothèse et termine la démonstration.

Ainsi la connaissance d'un élément α de norme égale à +/- 4 permet de trouver une solution. Si α est divisible par 2 dans A, 1/2.α est un élément de norme égale à +/- 1 et son carré est une solution. Sinon, 1/8.α³ est un élément de norme égale à +/- 1, un passage au carré permet encore de déterminer une solution.

Exemples

Exemple de Brahmagupta

Traitons avec cette méthode l'exemple de Brahmagupta suivant :

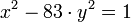
Choisissons comme premier essai α = 9 + √83 On remarque que N(α) = -2. Il est judicieux de calculer α² :

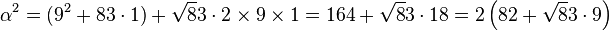
Une proposition précédente montre que 82 + √83.9 possède pour norme 1 et (82, 9) est solution de l'équation, en effet :

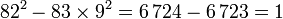
Défi de Fermat

Le défi de Fermat se résout de la même manière :

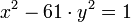
Brahmagupta s'y prend de la manière suivante, il remarque que si α = 39 + 5.√61 alors N(α) est égal à -4. Bien évidemment le formalisme de Brahmagupta n'a rien à voir avec celui utilisé ici, même si les calculs sont les mêmes. Il calcule 1/2.α² :

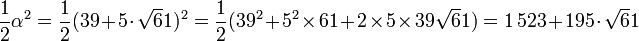
Puis il calcule 1/8.α³ et sa norme :

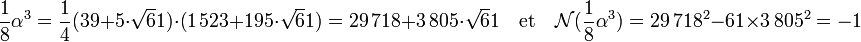
La solution est donc 1/64.α⁶, soit :

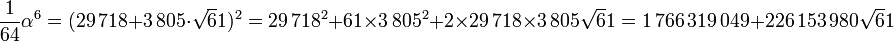
La méthode est remarquablement économique pour un algorithme aussi ancien.