Groupe des unités d'un anneau d'entiers quadratiques - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

En mathématiques, et plus précisément en théorie algébrique des nombres, le groupe des unités d'un anneau d'entiers quadratiques est composé de tous les éléments de l'anneau ayant un inverse pour la multiplication. Cet ensemble, munis de la multiplication, forme une structure de groupe abélien.
Un anneau d'entiers quadratiques est un anneau unitaire, c'est-à-dire une structure disposant de deux opérations, l'addition et la multiplication inclus dans l'ensemble des nombres complexes, et tel que tous les éléments soit composés d'entiers algébriques c'est-à-dire d'élément racine de polynômes à coefficients dans les entiers relatifs et dont le coefficient du monôme dominant est égal à 1. Dire que l'anneau est unitaire revient à dire que 1 est élément de l'anneau.
La structure du groupe dépend de la nature du corps quadratique. S'il contient des éléments non réels, c'est-à-dire dont la composante imaginaire pure n'est pas réduite à 0, alors le groupe est cyclique. Dans le cas contraire, le corps est dit totalement réel et le groupe est isomorphe, soit à Z/2Z.
Un tel groupe représente ce que Dirichlet appelle une obstruction, s'il est trop vaste, ce qui est le cas pour les corps quadratiques totalement réels. À la différence des autres nombres, il n'est pas possible de décomposer une unité en facteurs premiers. Il est parfois utile de bien connaître la structure du groupe des unités. Il est l'objet d'un théorème dit des unités de Dirichlet qui s'applique à tous les groupes des unités des anneaux d'entiers algébriques qui généralise la notion d'entiers quadratiques.
Les applications de la connaissance du groupes des unités sont diverses en arithmétique. L'équation de Pell-Fermat est une équation diophantienne, c'est-à-dire à coefficients entiers et dont les solutions recherchées sont entières dont la résolution d'un cas particulier revient exactement à la détermination du groupe des unités d'un anneau d'entiers quadratiques. La démonstration du dernier théorème de Fermat pour des valeurs pas trop particulières du paramètre n demande l'explicitation des racines nièmes de l'unité d'un anneau d'entiers algébriques. Dans le cas où n est égal à 3 ou à 5, certaines démonstrations utilisent des anneaux d'entiers quadratiques. Enfin l'article Entier quadratique de Q(√5) montre que l'étude de son groupe des unités permet une démonstration de la loi d'apparition des nombres premiers dans la suite de Fibonacci.
Structure du groupe des unités
Décors
Dans tout l'article, Z désigne l'anneau des entiers relatifs, Q le corps des nombres rationnels, R celui des nombres réels et C celui des complexes. Pour tout anneau d'entiers quadratiques, l'article détaillé montre l'existence d'un entier ω tel que l'anneau est égal à Z[ω], c'est-à-dire composé des éléments de la forme a + b..ω, où a et b sont des entiers. La valeur ω peut prendre deux formes distinctes, il existe un entier non carré parfait d tel que ω est égal à √d ou, si d est congru à 1 modulo 4, ω peut être égal à 1/2(1 + √d). L'entier d peut être négatif, la justification du radical √ associé à un nombre strictement négatif se trouve dans l'article détaillé. L'anneau des entiers est inclus dans le corps Q[ω] composé des éléments de la forme a + b..ω, où a et b sont des rationnels. Le corps Q[ω] est égal à Q[√d].
L'application conjuguée désigne celle qui à un élément de Q[√d], c'est-à-dire un élément du corps quadratique, a + b.√d associe a - b.√d. DAns la suite de l'article, le conjugué d'un entier quadratique α est noté αc. Cette application est un automorphisme de corps et sa restriction à l'anneau Z[ω] est aussi un automorphisme (cette fois d'anneau). L'application norme associe à un élément du corps le produit de cet élément avec son conjuguée. La norme est à valeur dans les nombres rationnels. La restriction de la norme à l'anneau des entiers est à valeur dans Z. L'expression de la norme est la suivante :
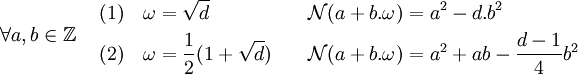
Une première propriété permet d'y voir un peu plus clair sur le groupe des unités :
-
- Un élément de l'anneau Z[ω] est inversible si, et seulement si, sa norme est, en valeur absolue égale à 1, l'inverse du nombre est alors soit son conjugué soit l'opposé de son conjugué.
En effet, soit α un élément de Z[ω]. S'il est de norme 1, alors soit α.c, soit α(-αc) est égal à 1. Comme α' et -αc sont élément de l'anneau, α est bien inversible. Réciproquement supposons que β soit l'inverse de α, alors la norme de α.β est égale à 1. La norme de α est un entier qui divise 1. Il n'en existe que 2, soit 1 soit -1. Ce qui démontre la proposition.
Remarque, si d est sans facteur carré, et, si dans le cas où d est congru à 1 modulo 4, ω est égal à 1/2(1 + √d) alors l'anneau est un peu particulier car il est la fermeture intégrale du corps quadratique. Cette spécificité n'intervient pas ici.
Théorème des unités de Dirichlet
Ce théorème structurant est un cas particulier de celui démontré par Dirichet sur l'anneau des entiers d'un corps algébrique quelconque. Deux configurations se présentent. Soit d est négatif, l'anneau n'est pas inclus dans R et la situation est relativement simple :
-
- Si d est négatif, le groupe des unités est un groupe cyclique. Il contient 4 éléments si d = -1, 6 si d = -3 et 2 sinon.
La situation est plus complexe si d est positif, l'anneau est inclus dans R et le groupe des unités est infini :
-
- Si d est positif, le groupe des unités est isomorphe au produit direct d'un groupe cyclique d'ordre deux et d'un groupe monogène d'ordre infini.
Un groupe monogène d'ordre infini est isomorphe à celui des entiers relatifs Z, le groupe des unités est isomorphe à Z/2.Z, le groupe des unités est isomorphe à Z/2Z x Z. Si le groupe isomorphe choisi est additif, le groupe des unités est évidemment multiplicatif.
Un exemple de groupe des unités d'ordre infini est donnée dans l'article Entier du corps quadratique Q(√5).
-
- Si d est négatif, le groupe des unités est cyclique et inclus dans celui des racines de l'unité :
Si d est égal à -1, le groupe est cyclique d'ordre 4 (cf Entier de Gauss), si d est égal à -3, le groupe est cyclique d'ordre 6 (cf Entier d'Eisenstein).
Sinon, il suffit de chercher les éléments de norme ±1. La norme d'un entier quadratique a + b.ω est soit égal à a2 - d.b2 si d n'est pas congru à 1 modulo 4, soit à (a - 1/2b)2 - d.b2/4 sinon. On remarque qu'elle est la somme de deux termes positifs, elle est donc positive. Si d est égal à -2, il n'est pas congru à 1 modulo 4 et il est de la forme a2 - d.b2. Le terme - d.b2 ne peut que être nul si a + b.ω est une unité, les deux seules valeurs possibles de a étant ±1. Ce raisonnement s'applique encore pour les cas restants, c'est-à-dire ceux où |d| est strictement plus grand que 4.
-
- Si d est strictement positif, le groupe des unités est isomorphe au produit direct d'un groupe cyclique d'ordre deux et d'un groupe monogène d'ordre infini :
Le groupe des unités de Z[ω] est noté Z[ω]*. On note αc le conjugué de α, si α est un élément de Q[ω] et soit ψ l'application de Q[ω]* dans R2 qui à α associe (ln(|α|), ln(|αc|)), ici ln désigne la fonction logarithme. L'application ψ est un morphisme du groupe multiplicatif (Q[ω]*, .) dans le groupe additif (R2, + ). La restriction de ψ à Z[ω]* est aussi un morphisme de groupe. Enfin, soit H le sous-espace vectoriel de R2 des couples (x, y) tel que x + y soit égal à zéro. On remarque qu'un élément de Z[ω] est une unité si, et seulement si son image est dans H.
-
-
- Le noyau de la restriction de ψ à Z[ω]* est le groupe cyclique d'ordre deux {-1, 1} :
-
Le noyau de la restriction est composé des éléments α de Z[ω]* tel que le logarithme de la valeur absolue de α et de αc soit égal à zéro. En conséquence α est égal à ±1.
-
-
- L'image de Z[ω]* par ψ est un sous-groupe discret de H :
-
Il suffit pour cela de montrer qu'il n'existe un ensemble fini de points de norme (au sens euclidien) bornée, c'est-à-dire inférieure à un réel strictement positif B. Soit α un élément de Z[ω]* dont l'image par ψ est de norme inférieure à B et a, b les deux entiers relatifs tel que α = a + b.ω. On remarque que la norme euclidienne de αc est égale à celle de α et donc est plus petite que B. La valeur 2.a est égal à α + αc et est inférieur à 2B, de même 2.b est égal à α - αc est aussi inférieur à 2.B. Il n'existe qu'un nombre fini d'éléments de Z[ω] satisfaisant ces deux propriétés, il n'en existe a fortiori qu'un nombre fini dans Z[ω]*. L'image de Z[ω]* par ψ est donc un sous-groupe discret de H.
-
-
- Soit un nombre réel B strictement positif, il existe une infinité d'éléments de Z[ω] dont la norme en valeur absolue est plus petite que B.
-
L'argument utilisé est géométrique, il correspond à l'usage du théorème de Minkowski sur un réseau, ici de R2. Un réseau de R2 est un sous-groupe discret. Graphiquement, il correspond à un quadrillage constitué par les 4 sommets n.u + m.v où u et v sont deux vecteurs libres de R2 et n et m des éléments de Z. Le volume fondamental du réseau est égal à la surface du parallélogramme constitué par les quatre points 0, u, v, u + v. Le théorème de Minkowski indique qu'un rectangle centré en (0,0) et de surface strictement supérieure à 4 fois celle du volume fondamental contient au moins un point du réseau différent du point nul.
On construit une suite de points correspondant à des éléments αn de Z[ω], dont la norme est en valeur absolue toujours plus petite que B, et une suite de rectangles. La largeur du rectangle diminue chaque fois suffisamment pour être certain que les points précédents de la suite d'éléments de Z[ω] ne puissent faire partie du nouveau rectangle. La hauteur du rectangle augmente suffisamment pour que le théorème de Minskowski nous assure de l'existence d'un point de Z[ω] dans le nouveau rectangle.
Soit φ, l'application de Q[ω] dans R2, qui à un élément α associe (α, αc). L'image de Z[ω] par φ est le réseau de R2 engendré par les vecteurs (1, 1) et (ω, ωc) car (1, ω) forme une base du Z module Z[ω]. Le volume fondamental V du réseau est égal à la surface du parallélogramme de sommets 0, (1,1), (ω, ωc) et (1 + ω, 1 + ωc). Un rapide calcul montre que V est égal à 2.√d.
On considère la suite de rectangles Rn centrés en 0 de longueur 2.tn et de hauteur 2(V + 1)/tn. Leurs surfaces sont toujours égales à 4(V + 1) et ils contiennent nécessairement un point de l'image de Z[ω] d'après le théorème de Minskowski. Un point β de Z[ω] dont l'image par φ est dans le rectangle Rn, possède une valeur absolue inférieure à tn et un conjugué de valeur absolue inférieure à 2(V + 1)/tn. Sa norme est en conséquence bien bornée par 2(V + 1), égal à la constante B recherchée.
Définissons par récurrence les suites (tn), correspondant à la demi-longueur des rectangles et αn la suite des points de Z[ω] dont l'image est dans Rn. On pose t0 = 1 et α0 un point non nul de Z[ω] et dont l'image est dans R0. Supposons les deux suites définies à l'ordre n. Soit tn+1 un réel strictement positif et strictement inférieur à la valeur absolue de αn. Le rectangle Rn+1 ne contient aucune image des αj si j est inférieur ou égal à n car sa longueur est strictement plus petite que la valeur absolue du plus petit des αj, qui forme une suite décroissante en valeur absolue. En revanche, sa surface, égale à 4(V + 1) garantit, d'après le théorème de Minkowski, l'existence d'un point αn+1 non nul dont l'image est à l'intérieur du rectangle Rn+1. La suite (αn) est bien une suite infinie de points distincts dont la norme est strictement inférieure à une constante B.
-
-
- Il existe deux indices i et j distincts et une unité ε de Z[ω] tel que αi = ε.αj :
-
Pour cela, il est utile de considérer l' ensemble des multiples de αn, si n est un entier quelconque. Un tel ensemble est appelé idéal principal engendré par αn, il est en général noté αn.Z[ω] et ici Jn pour une raison de simplicité. La technique utilisée ici consiste à étudier l'anneau quotient An = Z[ω]/Jn. Le paragraphe Idéal premier, idéal maximal de l'article Idéal de l'anneau des entiers d'un corps quadratique montre cet anneau quotient est de cardinal fini.
Il n'existe qu'un nombre fini d'anneaux, à un isomorphisme près, pour un cardinal donné. Pour s'en persuader, il suffit de considérer que le nombre de tables de multiplications et d'additions est fini. Ensuite un morphisme de Z[ω] dans un anneau unitaire An est entièrement défini par l'image de ω. En effet, l'image de l'unité de Z[ω] est nécessairement l'image de l'unité de An et tout élément de Z[ω] s'exprime comme la somme d'un itéré de 1 et de ω. Il n'existe donc qu'un nombre fini de morphismes de Z[ω] dans An, inférieur ou égal à B2, c'est-à-dire le nombre d'images que peut prendre ω. Les différents idéaux correspondent aux différents noyaux des morphismes. Il n'en existe qu'un nombre fini.
Soit i et j deux indices tels que les idéaux engendrés par αi et αj soient les mêmes. Il en existe car le nombre d'indice est infini à la différence du nombre d'idéaux. αi est un multiple de αj, il existe donc un élément ε de Z[ω] tel que αi = ε.αj. De même, αj est un multiple de αi, il existe un élément ε1 de Z[ω] tel que αj = ε1.αi. En remplaçant l'expression de αj dans la première égalité on trouve αi = ε.ε1.αi et donc ε.ε1 = 1. Comme αi et αj ont été choisi distincts ils sont de valeurs absolues différentes. On en déduit que ε, égal au quotient αi/αj, ne peut être égal à ±1. On a bien montré l'existence d'une unité différente de ±1.
-
-
- Le groupe des unités est isomorphe à Z/2Z x Z :
-
L'image de Z[ω]* par ψ est isomorphe à Z, son noyau est isomorphe à Z/2Z. Soit v un élément tel que ψ(v) soit générateur de l'image. L'application de Z/2Z x Z dans Z[ω]*, qui à (p, n) associe (-1)p.ωn est un isomorphisme, ce qui démontre le théorème.
Structure géométrique
La structure géométrique ne fait véritablement sens que dans le cas où d est négatif, celui étudié ici. Il est possible de considérer (1, ω) comme une base du Q espace vectoriel Q[√d]. On peut de plus définir cette base, comme orthonormale. Tout élément α = x + y.ω vérifie l'une des deux équations :
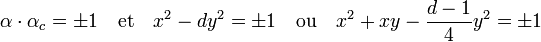
Dans les deux cas, on observe que chaque unité se trouve sur une des quatre branches de deux hyperboles tournées d'un quart de tour, l'une par rapport à l'autre. Les unités sont les intersections des hyperboles avec les sommets du quadrillages correspondant au réseau Z[ω].
À chaque solution α = a + b.ω, il en existe trois autres associées αc, -α et -αc. Il en existe une par quadrant. Le premier quadrant est formé par les points d'abscisses positives et d'ordonnées strictement positives et les autres sont obtenus par rotation d'un quart de tour.
Une solution particulièrement intéressante est celle satisfaisant la définition suivante :
-
- Une unité ρ est dite primitive ou fondamentale lorsque, pour toute unité α il existe un entier e égal à 1 ou -1 et un entier relatif k tel que α soit égal à e.ρ k.
Il existe quatre unités fondamentales : ρ, ρc, -ρ et -ρc, selon le théorème de Dirichlet. En général, on recherche celle présente dans le premier quadrant. Si ρ est dans le premier quadrant alors ρn l'est aussi, ρ-n se trouve sur le quadrant des abscisses positives et ordonnées négatives, -ρ-n possèdent des abscisses négatives et des ordonnées positives et -ρn possèdent abscisses et ordonnées négatives. On peut remarquer que c'est l'unité différente de 1 qui possède la plus petite abscisse du premier quadrant (abscisses et ordonnées positives). En effet, si α = a + b.ω est l'unité primitive telle que a et b soient positifs, et β = c + e.ω une unité tel que α.β soit différent de 1 et toujours dans le premier quadrant. L'unité β possède nécessairement des coordonnées positives et le produit des deux unités a pour abscisse a.c + (d - 1)/4.b.e ou a.c + d.be qui est clairement supérieur à a.