Groupe fondamental - Définition

Définition

Classe d'équivalence de lacets

Soit X un espace topologique. Un arc continu est une application continue γ : [0 1] → X.

Soit p un point fixé dans X. Un lacet basé en p est un arc continu vérifiant de plus γ(0) = γ(1) = p.

Deux lacets γ₀ et γ₁ sont dits homotopes s'il existe une homotopie de l'un vers l'autre, c'est-à-dire une application continue H : [0 1]² → X telle que :

• 
• 
• .

La dernière condition exprime que pour x fixé entre 0 et 1 γ_x(t) = H(t,x) est un lacet basé en p.

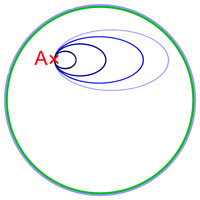
Autrement dit, deux lacets sont dit homotopes si l'on peut passer continument de l'un à l'autre, à l'image de la figure de droite (le point p est situé en A sur la figure) .

Le fait d'être homotopes est une relation d'équivalence entre lacets (basés en p). On peut considérer l'ensemble E(p) des lacets (basés en p) de X et l'ensemble quotient π₁(X,p) de E(p) par la relation d'homotopie. On notera [γ] la classe d'équivalence d'un lacet γ (aussi appelée classe d'homotopie).

Intuitivement (si l'espace X est métrisable et localement compact) une classe d'homotopie de lacets est une composante connexe par arcs de l'espace E(p) muni de la topologie de la convergence compacte-ouverte. π₁(X,p) est l'ensemble des classes d'équivalence d'homotopie [γ] de lacets basés en p. C'est donc l'ensemble des composantes connexes par arcs de E(p).

Structure de groupe

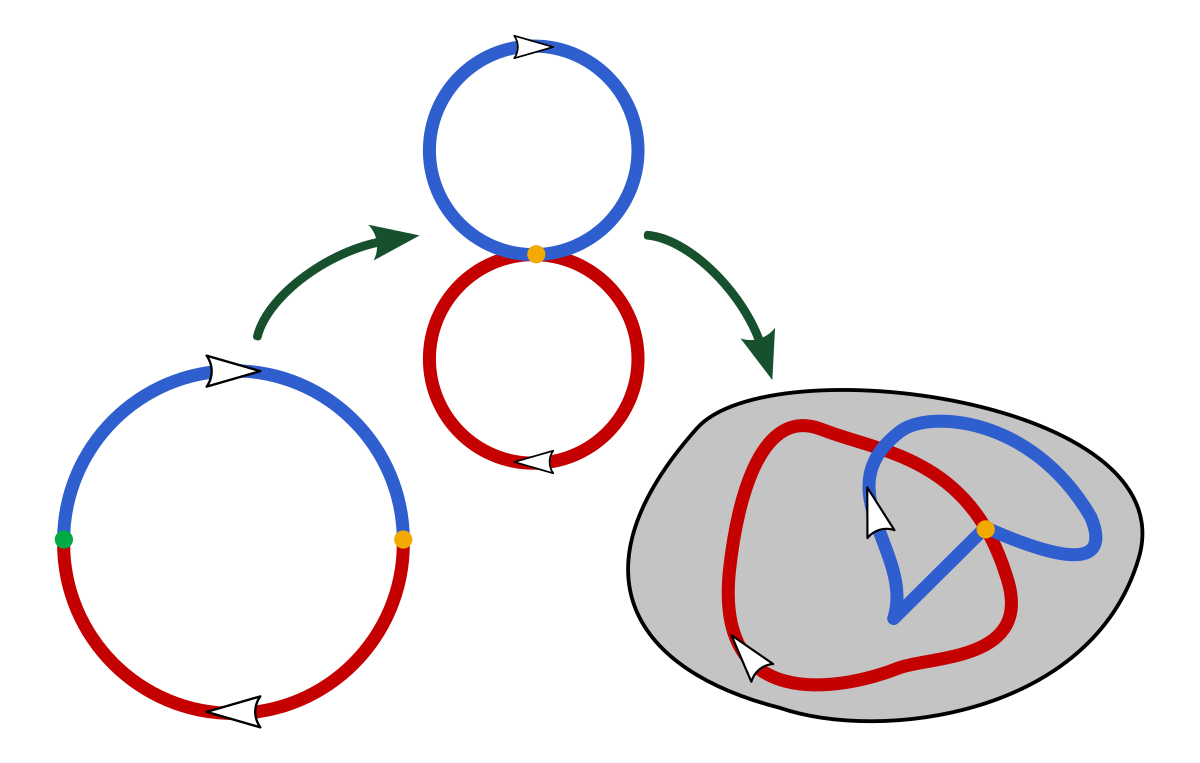
On souhaite donner une structure de groupe à cet ensemble π₁(X,p). Si f et g sont deux lacets de X (basés en p), leur concaténation est le lacet h défini par :

Intuitivement, c'est le lacet qui parcourt f puis g (chacun à vitesse double, pour arriver à parcourir le lacet en un temps unité). On notera fg le concaténé de f et de g. On peut prouver que la classe d'homotopie [fg] ne dépend que de la classe d'homotopie de f, et de celle de g. Ainsi, on peut définir une loi de composition interne sur l'ensemble π₁(X,p) des classes d'homotopie des lacets basés en p de X, par [f][g] = [fg].

On peut alors prouver que l'on obtient une structure de groupe sur l'ensemble π₁(X,p) : la loi est associative car les lacets (fg)h et f(gh) sont homotopes, l'élément neutre est la classe d'homotopie [γ] du lacet trivial γ défini par γ(t) = p pour tout t. L'inverse d'un lacet f est simplement le même lacet, mais parcouru dans l'autre sens (c'est-à-dire, défini par f ^{− 1}(t) = f(1 − t))

Le groupe ainsi obtenu est appelé groupe fondamental (ou groupe de Poincaré) de X basé en p, et est noté π₁(X,p).

Point base

Examinons le cas particulier où l'espace topologique X est connexe par arcs. Deux groupes fondamentaux basés en deux points p et q (π₁(X,p) et π₁(X,q)) sont isomorphes. En effet, il existe un chemin γ allant de p à q. On peut donc définir l'application suivante

qui réalise visiblement un isomorphisme du groupe fondamental π₁(X,q) vers le groupe fondamental π₁(X,p) dont l'isomorphisme réciproque est l'application :

Ainsi, si X est connexe par arcs, par abus de langage, on parle du groupe fondamental (à un isomorphisme non unique près) de l'espace topologique X, sans préciser le point base, que l'on note π₁(X) = π₁(X,p). Cependant, l'isomorphisme entre les groupes π₁(X,p) et π₁(X,q) n'est pas unique et dépend du choix d'un chemin entre p et q . Ainsi on doit se souvenir que le groupe fondamental varie lorsque le point base varie dans l'espace X, les groupes restant toujours isomorphes.

Si X n'est pas connexe par arcs, les groupes fondamentaux de deux composantes connexes, sont différents. Par abus de langage, on parle néanmoins du groupe fondamental d'une composante connexe par arcs, sans préciser le point base, mais on doit se souvenir que le groupe fondamental varie lorsque le point base varie dans la composante connexe par arcs, les groupes restant toujours isomorphes. À l'inverse, un autre invariant d'un espace topologique, non nécessairement connexe par arcs, le premier groupe d'homologie, ne dépend pas du choix d'un point base ni du choix d'une composante connexe par arcs. Si le groupe fondamental (en un point) est abélien, ce qui est le cas de celui des groupes de Lie ou des espaces simplement connexes, il s'identifie naturellement au groupe d'homologie de la composante connexe du point.

Espaces simplement connexes

Un espace topologique connexe par arcs dont le groupe fondamental est trivial est dit simplement connexe .