Groupe fondamental - Définition

Généralisations

Groupoïde fondamental (ou groupoïde de Poincaré)

Une catégorie est appelée un groupoïde si les objets et les flèches forment un ensemble (c'est une "petite catégorie") et si toutes les flèches sont inversibles (sont des isomorphismes). Les groupoïdes forment une catégorie dont les morphismes sont les foncteurs entre groupoïdes. Les groupes sont des groupoïdes (avec un seul objet).

Soit G un groupoïde, on définit la relation d'équivalence si G(x,y) est non vide, elle définit un groupoïde quotient noté π₀(G). π₀ définit un foncteur (composantes connexes) de la catégorie des groupoïdes vers la catégorie des ensembles.

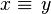
A chaque espace topologique on va associer de façon fonctorielle un groupoïde πX.

Soit X un espace topologique, on prend pour ensemble d'objets πX l'ensemble sous-jacent à X. Les flèches de source x et de but y sont les classes d'homotopie des chemins (= arcs continus) de x vers y. La relation d'homotopie est compatible avec la composition des chemins et définit donc un groupoïde πX appelé le groupoïde fondamental de X. Le théorème de Van Kampen s'exprime également simplement en utilisant les groupoïdes fondamentaux.

Soit G un groupoïde, et x un objet de G (on dit aussi un point de G). La loi de composition entre les flèches de G(x,x) restreinte à ce sous-groupoïde est une loi de groupe. On note π₁(G,x) ce groupe. Remarque : π₁ ne définit pas un foncteur de la catégorie des groupoïdes vers la catégorie des groupes.

Le groupe fondamental est défini par π₁(X,x₀) = π₁(πX,x₀)

Groupes d'homotopie supérieurs

Le groupe fondamental est en fait le premier groupe d'homotopie, d'où l'indice 1 dans la notation π₁(X).

Groupe fondamental et géométrie algébrique

Dans la théorie des revêtements d'un espace X, on définit la fibre d'un revêtement au point p comme l'ensemble qui est aussi noté E(p). La correspondance définit un foncteur de la catégorie des revêtements de base (X; p), dans la catégorie des ensembles. Le groupe fondamental peut être défini de manière abstraite comme le groupe des automorphismes du foncteur fibre, qui, à un revêtement de base (X,p), associe E(p).

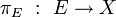
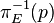
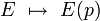
Cette définition alternative ouvre la voie à la généralisation en géométrie algébrique, où la définition donnée précédemment en termes de lacets de base p ne s'applique pas naturellement. Dans cette généralisation, les revêtements étant remplacés par les morphismes étales : le groupe fondamental de l'espace pointé (X,p) est le groupe des automorphismes du foncteur fibre qui, à un morphisme étale , associe la fibre E(p) au point p. Cette généralisation est due à Alexandre Grothendieck et Claude Chevalley.

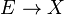
Cette théorie permet d'expliquer le lien entre la théorie de Galois des revêtements des surfaces de Riemann (groupe d'automorphismes…) et la théorie de Galois des corps de fonctions.

Méthodes de calcul et applications

Théorème de van Kampen

Calculer le groupe fondamental d'un espace topologique qui n'est pas simplement connexe est un exercice difficile, car il faut prouver que certains lacets ne sont pas homotopes. Le théorème de van Kampen, également appelé théorème de Seifert-Van Kampen, permet de résoudre ce problème lorsque l'espace topologique peut être décomposé en des espaces plus simples dont les groupes fondamentaux sont déjà connus. Ce théorème permet de calculer le groupe fondamental d'un éventail très large d'espaces.

En termes abstraits, ce théorème dit que si deux sous-espaces, tous les deux ouverts ou tous les deux fermés, de X contiennent le point p et ont une intersection connexe par arcs, le groupe fondamental de la réunion des deux espaces pointés en p est la somme amalgamée (dans la catégorie des groupes) des groupes fondamentaux des deux espaces, en p, somme amalgamée le long du groupe fondamental de leur intersection.

.

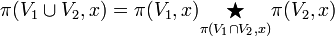
Théorème du cône et groupe fondamental des espaces projectifs

Si X est un espace topologique, on définit le cône de X comme l'espace quotient où I désigne le segment [O;1]. Si X est un cercle, on obtient une partie d'un cône de révolution. Le groupe fondamental du cône d'un espace connexe par arc est trivial, autrement dit, si X est connexe par arcs, C(X) est simplement connexe. On a une inclusion canonique .

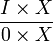
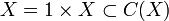
Si f est une application continue entre deux espaces topologiques , on définit le cône de l'application f : C(f) comme l'espace obtenu en recollant et le long de X.

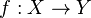
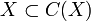
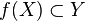
Exemple : Si f est l'application de degré 2 dans le cercle , on obtient . Le cône de f est le plan projectif réel.

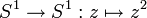
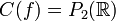
Le théorème du cône affirme que le groupe fondamental de C(f) est isomorphe au quotient de π₁(Y) par le normalisé du sous-groupe de π₁(Y) image de f.

Application : les espaces projectifs (réels) pour ont des groupes fondamentaux isomorphes à .

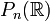
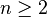
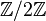
Groupe fondamental des graphes, des surfaces et des polyèdres

• Le groupe fondamental des graphes est un groupe libre.
• Le groupe fondamental des polyèdres admet une présentation par générateurs et relations. Une relation étant fournie par chacune des faces du polyèdre.
• Le groupe fondamental d'une surface compacte orientable admet une présentation avec 2g générateurs et une seule relation ( , on peut aussi choisir la présentation ). L'entier g est uniquement déterminé par la surface et est appelé genre de la surface.

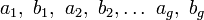
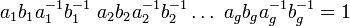
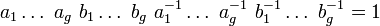
Théorie des nœuds

En théorie des nœuds, on cherche à distinguer les différents nœuds (ceux qui ne sont pas homotopiques). Le groupe fondamental du complémentaire d'un nœud fournit un invariant des nœuds, qui permet de distinguer certains d'entre eux.