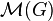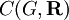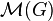Groupe topologique compact - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Exemples de groupes compacts - Représentation des groupes compacts - Intégration sur les groupes compacts

Intégration sur les groupes compacts

Sur tout groupe topologique localement compact et séparable G, il existe une mesure borélienne invariante par les translations à gauche, appelée mesure de Haar, unique à coefficient multiplicatif près. Elle est finie sur les parties compactes de G. Si G est lui-même compact, toute mesure de Haar est finie, et il est possible de la normaliser pour que sa masse vaille 1. On dispose ainsi sur tout groupe topologique compact G d'une unique mesure de probabilité qui soit invariante par translations à gauche, qu'on nomme par abus de langage la mesure de Haar de G, notée $λ$ dans la suite de l'article.

En pratique, la mesure de Haar permet de moyenner les objets sur G pour obtenir des objets invariants.

Unimodulaire

Un groupe topologique localement compact et séparable est dit unimodulaire si une (et donc toute) mesure de Haar est invariante à droite. Tout groupe topologique compact est unimodulaire.

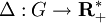
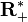
En général, le translaté à droite d'une mesure de Haar $λ$ par g est une mesure de Haar, donc s'écrit $Δ(g).λ$ . Le coefficient réel $Δ(g)$ est indépendant du choix de $λ$ et $\Delta:G\rightarrow \mathbf{R}_+^*$ est un morphisme continu de groupes topologiques. Si G est compact, l'image de $Δ$ est un sous-groupe compact de $\mathbf{R}_+^*$ : a fortiori, il est trivial. L'application $Δ$ est dans ce cas constante égale à 1. Toute mesure de Haar est invariante par les translations à droite.

Théorème du point fixe de Kakutani

Le théorème suivant a été démontré par Shizuo Kakutani en 1941 :

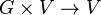
Théorème du point fixe de Kakutani : Soient V un espace vectoriel topologique localement convexe séparé, G un groupe topologique compact, et $G\times V\rightarrow V$ une action linéaire continue de G sur V. Supposons donnée une partie C convexe compacte non vide de V globalement stable par l'action de G. Alors il existe un point c dans C fixe par tous les éléments g de G (g.c=c).

Le théorème de Kakutani donne une preuve élémentaire de l'existence de la mesure de Haar sur un groupe compact G. En effet, l'espace des mesures réelles finies $\mathcal{M}(G)$ est par le théorème de Riesz le dual topologique de l'espace de Banach des fonctions continues réelles $C(G,\mathbf{R})$ , muni de la norme de convergence uniforme. Les mesures boréliennes de probabilité forment un sous-ensemble convexe et *-faiblement compact. L'action de G sur lui-même par translations à gauche induit une action linéaire de G sur $\mathcal{M}(G)$ , qui soit continue pour la topologie *-faible. Le convexe C est stable par G : de fait, le théorème de Kakutani s'applique et donne l'existence d'un point fixe de l'action de G dans C, autrement dit d'une mesure borélienne de probabilité sur G invariante par translation à gauche. L'existence de la mesure de Haar se trouve ainsi établie. (Cependant, la compacité ne permet pas de simplifier la preuve de l'unicité.)