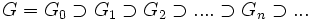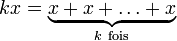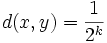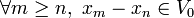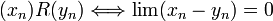Si
est un groupe abélien, si
est une suite de sous-groupes de
telle que:
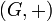
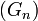
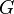
Alors la suite
induit une topologie sur
dans laquelle les voisinages de
sont les parties de
contenant un des ensembles
.
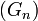
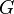
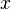
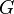
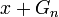
Si de plus, l'intersection des
est réduite à
où
est l'élément neutre de
, le groupe est séparé.
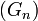
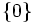
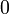
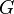
Un cas particulier de groupe topologique de cette forme est le groupe muni de la topologie p-adique: Si
est un entier naturel, la suite
est définie par
. (on rappelle que, pour tout entier naturel
et tout élément
de
, l'élément
est défini par
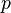
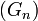
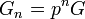
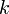
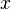
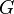
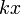
Distance induite
On peut définir une distance sur
muni de la topologie induite par
si l'intersection des
est bien réduite à
:
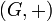
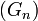
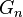
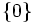
où
est le premier entier tel que
et
si pour tout entier
,
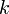
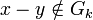
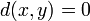
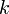
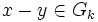
Complété
Si
est un groupe abélien séparé muni de la topologie déterminée par la suite
, on peut définir dans
des suites de Cauchy. Une suite
est de Cauchy si et seulement si, pour tout voisinage
de 0, il existe un entier
tel que
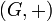
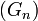
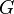
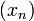
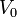
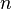
Sur cet ensemble de suites de Cauchy noté
on peut définir une relation d'équivalence:
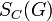
Le groupe quotient
est alors un espace complet. Le groupe
est alors isomorphe à un sous-groupe dense de
.
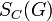
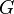
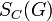
L'exemple le plus important d'une telle construction est celui des nombres p-adiques : on fait cette construction à partir de
et de la multiplication par un nombre premier
.
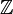
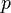
Cette construction du complété se généralise, dans le cadre uniforme, à tout groupe topologique abélien séparé
