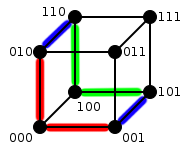
Hypercube (graphe) - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Fondamentales
- Degré. Deux sommets sont connectés s'ils diffèrent exactement sur un symbole de leurs étiquettes. Comme l'étiquette a n symboles, chaque sommet est connecté à exactement n voisins : tout sommet a donc degré n, autrement dit le graphe est n-régulier.
- Nombre de sommets. Par la construction récursive, on voit que pour passer de Qn − 1 à Qn, il faut faire une copie du graphe, autrement dit le nombre de sommets est doublé. Si Vn est le nombre de sommets du graphe Qn, on obtient ainsi Vn = 2 * Vn − 1, et le premier cas est V1 = 2 ; en déroulant la récurrence, on obtient Vn = 2 * Vn − 1 = 22 * Vn − 2 = ... = 2n, c'est-à-dire que le graphe a 2n sommets.
- Diamètre. Une des propriétés du produit cartésien est que le diamètre D(C) de
- Cycles. Par construction, le plus petit cycle correspond à Q2, qui est isomorphe au cycle C4 (i.e. le cycle de longueur 4). Le graphe Q3 est formé par deux graphes Q2 : si l'on souhaite un cycle de longueur supérieur à 4 dans Q3, alors on choisit p arêtes dans un des deux graphes Q2, p arêtes dans l'autre Q2 et 2 arêtes supplémentaires pour naviguer entre les deux graphes, ce qui porte le total d'arêtes à
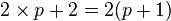
- Nombre chromatique. Un graphe est biparti si et seulement si il ne contient pas de cycle impair, et il découle donc de la propriété précédente que l'hypercube est biparti. Un graphe biparti est celui pouvant être colorié avec deux couleurs, et ainsi le nombre chromatique de l'hypercube est χ(Qn) = 2. Pour voir qu'un graphe est biparti, il suffit de trouver un schéma afin de ranger chaque sommet dans un ensemble G1 ou G2, de façon telle que tout sommet d'un ensemble ait comme voisins uniquement des sommets de l'autre ensemble. Dans le cas de l'hypercube, l'ensemble G1 peut être constitué des sommets dont l'étiquette a un nombre pair de 1, et G2 est l'ensemble de sommets dont l'étiquette a un nombre impair de 1. Un sommet étant connecté à tous ceux dont l'étiquette diffère exactement d'un symbole, il en découle que le nombre de 1 des voisins d'un sommet est soit supérieur soit inférieur : ainsi, un sommet pair sera connecté à des sommets impairs, et vice-versa.
- Planaire. L'hypercube est planaire (c'est-à-dire pouvant se dessiner sur un plan sans croiser deux arêtes) uniquement pour
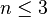
- Eulérien. Un graphe a un chemin eulérien si et seulement si tout sommet est de degré pair. Comme Qn est n-régulier, il en résulte qu'il n'y a un chemin eulérien que pour n pair.
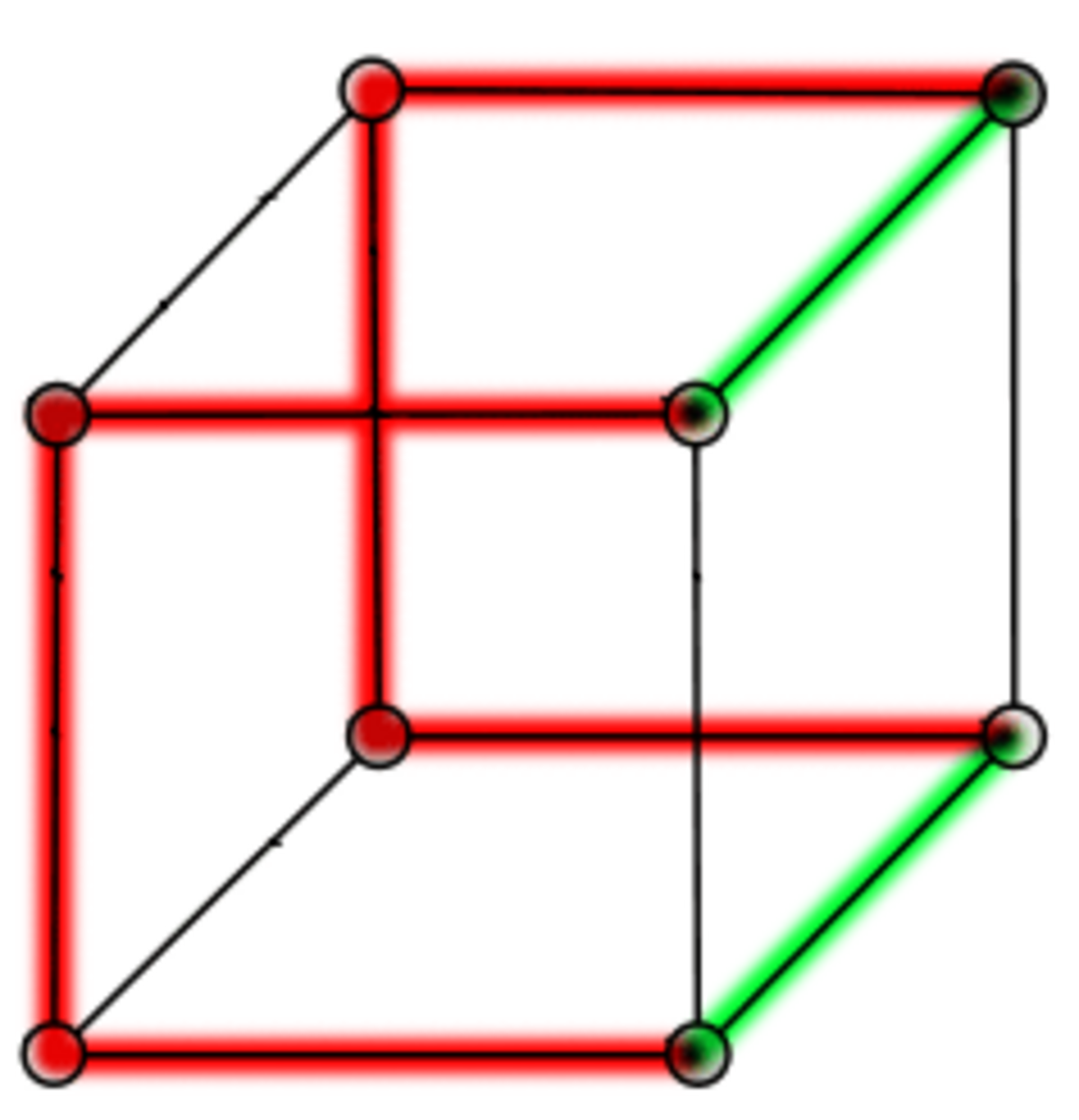
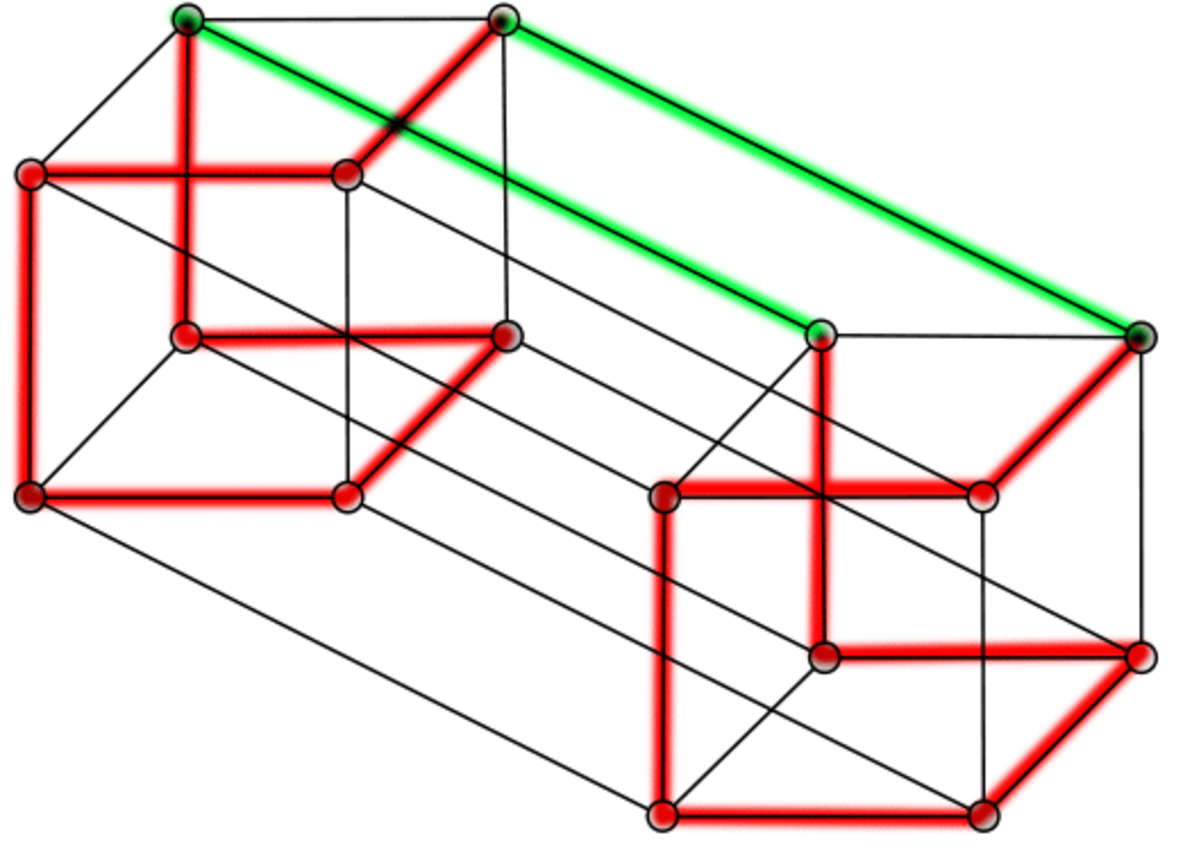
- Hamiltonien. Q2 étant un cycle, il est aussi un circuit hamiltonien. Pour construire un circuit hamiltonien dans Q3, on sait qu'il y a un circuit hamiltonien dans le graphe d'origine et dans sa copie : supprimons une arête dans chacun de ces circuits et raccordons les sommets ainsi libérés pour créer un circuit hamiltonien dans l'ensemble. Ce processus est illustré ci-dessous pour Q3 et Q4. Le nombre exact de cycles hamiltoniens est donné ci-dessous pour les premiers hypercubes ; au-delà, l'estimation la plus précise quant au nombre k de circuits hamiltoniens dans Qn est donnée par :
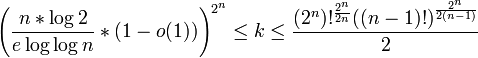
| n | Sans compter les cycles isomorphes | En comptant tous les cycles |
|---|---|---|
| 2 | 1 | 1 |
| 3 | 1 | 6 |
| 4 | 9 | 1344 |
| 5 | 275 065 | 906 545 760 |
- Graphe de Hamming. Un graphe de Hamming H(d,q) est le graphe obtenu par produit cartésien de d graphes complets Kq. L'hypercube Qd étant obtenu par produit cartésien de d copies de K2, il découle de la définition que tout hypercube Qd est isomorphe à H(d,2). Une définition alternative d'un graphe de Hamming montre le rapport direct avec celle utilisée pour introduire l'hypercube : H(d,q) est le graphe dont les sommets sont Sd, l'ensemble des mots de longueur d sur un alphabet S, où | S | = q. Deux sommets sont adjacents dans H(d,q) s'ils sont à une distance de Hamming de 1, c'est-à-dire si leurs étiquettes ne diffèrent que d'un symbole.
- Distance-régulier. Un hypercube est un graphe distance-régulier et son vecteur d'intersection est {n,n − 1,n − 2,...,1,1,2,3,...,n}.
- Diagramme de Hasse. L'hypercube Qn est isomorphe au diagramme de Hasse d'une algèbre de Boole à n éléments.
- Reconnaissance. Étant donné une liste d'adjacence, on peut savoir en temps et espace linéaire si le graphe qu'elle représente est un hypercube.
- Code de Gray. Les étiquettes ordonnées des sommets dans un cycle hamiltonien sur Qn définissent le code de Gray sur n bits. De plus, ce code suit une construction similaire à celle de l'hypercube : les mots de n bits sont déterminés en copiant les mots de n − 1 puis en rajoutant 0 devant l'original, 1 devant la copie, et en inversant les mots de la copie.
- Distance-unité. L'hypercube est un graphe distance-unité : il peut s'obtenir à partir d'une collection de points du plan euclidien en reliant par une arête toutes les paires de points étant à une distance de 1.
Aspects algébriques
Groupe d'automorphisme
Le groupe d'automorphisme Γ(Qd) de l'hypercube Qd est d'ordre 2dd!. Il est isomorphe au produit en couronne des groupes symétriques S2 et Sd :
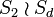
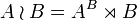
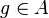
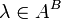
L'hypercube Qd est un graphe arc-transitif : son groupe d'automorphisme Γ(Qd) agit transitivement sur l'ensemble de ses arcs. Étant donné deux arêtes e1 = u1v1 et e2 = u2v2 de G, il existe deux automorphismes
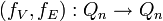
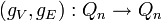
L'hypercube Qd est donc a fortiori symétrique. Le groupe Γ(Qd) agit donc également transitivement sur l'ensemble de ses sommets et sur l'ensemble de ses arêtes. En d'autres termes, tous les sommets et toutes les arêtes d'un hypercube jouent exactement le même rôle d'un point de vue d'isomorphisme de graphe.
Le graphe hexaédrique (Q3) est l'unique graphe cubique symétrique à 8 sommets. Le graphe tesseract (Q4) est l'unique graphe symétrique régulier de degrés 4 à 16 sommets.
Graphe de Cayley
L'hypercube Qd est un graphe de Cayley Cay(G, S) avec :
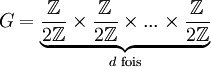
Cela découle d'une propriété plus générale statuant que tous les graphes de Hamming sont des graphes de Cayley.
Matrice d'adjacence et spectre
La matrice d'adjacence A(Q2) de l'hypercube Q1 est définie ci-dessous. Par la définition récursive de l'hypercube, pour passer à la dimension supérieure Q2, on duplique Q1 et connecte les sommets d'origine à leur équivalent dans la copie.
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
On obtient ainsi la matrice d'adjacence A(Q3) ci-dessous :
| 00 | 01 | 10 | 11 | |
|---|---|---|---|---|
| 00 | 0 | 1 | 1 | 0 |
| 01 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 0 | 1 |
| 11 | 0 | 1 | 1 | 0 |
Au niveau de la matrice, l'opération passant de Q1 à Q2 se comprend comme suit : les entrées {A00 − 00,A00 − 01,A01 − 00,A01 − 01} correspondent à la matrice d'origine, et se trouvent dupliquées en {A10 − 10,A10 − 11,A11 − 10,A11 − 11}. Dans les autres entrées, on connecte chaque sommet à sa copie. Ainsi, la forme générale de la matrice est donnée de la façon suivante, où
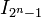
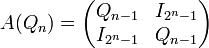
Pour comprendre l'évolution du spectre de la matrice en fonction de n, il faut revenir à la définition comme produit cartésien. Le spectre d'un produit cartésien

Chemins et sous-graphes
Pour aller d'un sommet à un autre, on utilise à nouveau le fait que deux sommets sont connectés s'ils diffèrent exactement sur un symbole de leurs étiquettes. Ainsi, un chemin est trouvé en faisant correspondre une à une les coordonnées du sommet de destination avec celui d'origine. Par exemple, pour aller de 0010 à 1011, on obtient
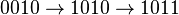
Notons deux choses. Premièrement, la longueur d'un chemin entre deux sommets est le nombre de symboles sur lesquels leurs étiquettes diffèrent : ainsi, si les étiquettes sont complètement différentes, le chemin sera de longueur n, ce qui est une autre explication quant au diamètre du graphe. Deuxièmement, le chemin choisi n'est pas unique : au lieu d'aller de 0010 en 1010, on aurait tout d'abord pu passer par 0011 avant d'aller en 1011. Le nombre de chemins différents pour aller entre deux sommets est un problème de combinatoire : considérons que les sommets diffèrent sur k symboles, combien de façons a-t-on de générer des chemins ? On a k choix pour le premier symbole à changer, puis k − 1 choix pour le second symbole à changer, jusqu'à un seul choix quand il n'y a plus qu'un symbole à changer ; ainsi, le nombre de chemins entre deux sommets différant sur k symboles est k!.
Hypercubes induits
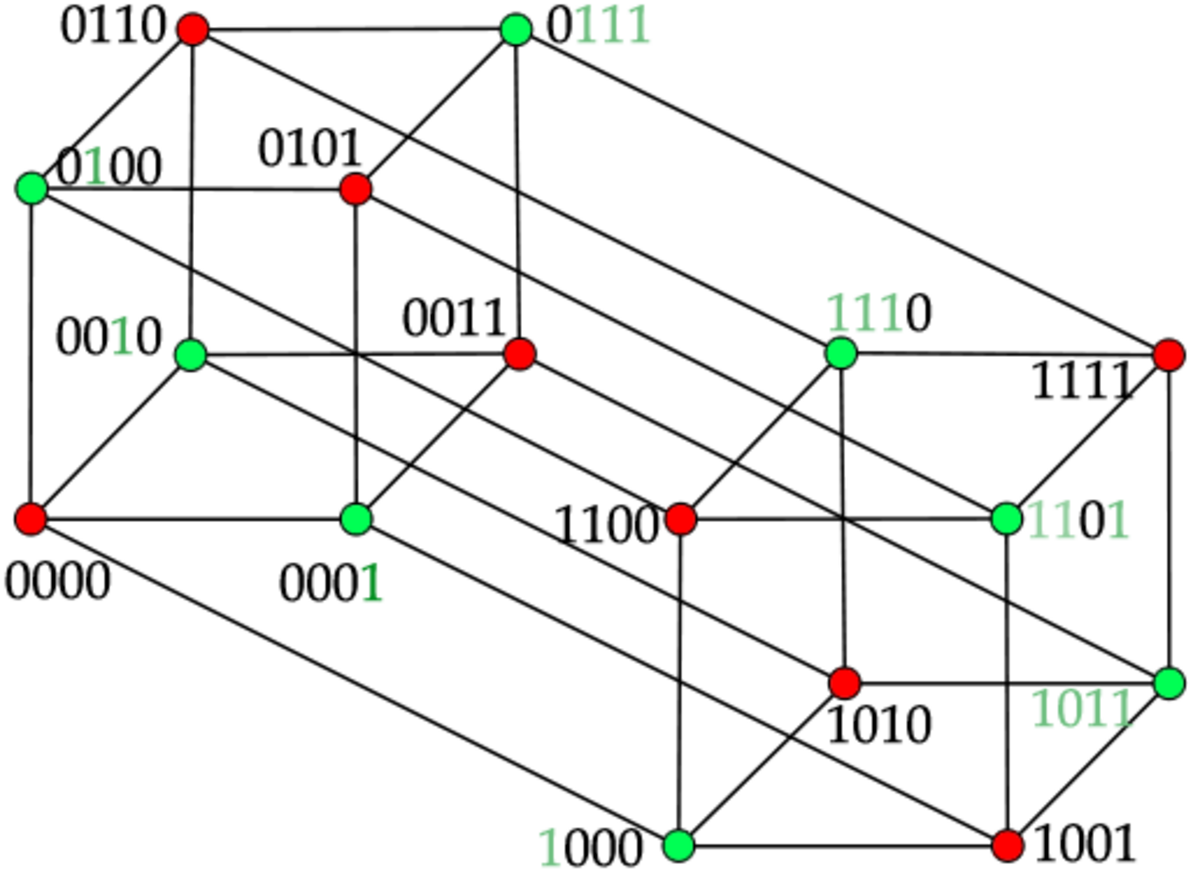
Les chemins entre deux sommets ont d'autres propriétés intéressantes, particulièrement pour les sous-graphes qu'ils définissent. Ainsi, l'union des chemins entre deux sommets distants de k (i.e. différant de k symboles) donne l'hypercube Qk. Ceci est illustré par l'exemple ci-dessous : dans le cas de deux sommets voisins u et v, il n'y a qu'un chemin et on obtient l'hypercube Q1 ; dans le cas où ils sont à distance 2, il y a deux chemins entre eux qui définissent Q2, et s'ils sont à distance 3 alors l'union des chemins représente l'ensemble de l'hypercube Q3.
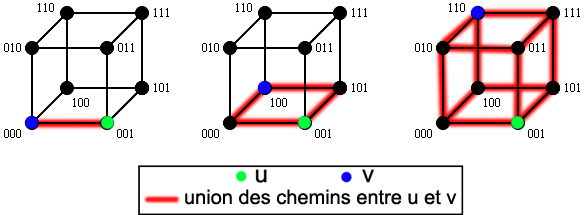
Le nombre αd d'hypercubes Qd compris dans Qn est donné par la formule suivante :
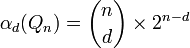
L'hypercube est aussi un graphe médian, et en particulier le seul graphe médian régulier. On peut donc appliquer la formule suivante des graphes médians :
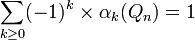
Spanners
Certains types de sous-graphe sont particulièrement utiles en termes de communications. Par exemple, un spanner est un sous-graphe couvrant, c'est-à-dire qui contient tous les sommets, mais qui contient moins d'arêtes. Contenir moins d'arêtes peut augmenter les distances entre des sommets du graphe, et l'on distingue ainsi les spanners multiplicatifs, où la distance peut être multipliée par un facteur k, des spanners additifs où la distance peut être augmentée d'un montant k. Dans le cas d'un spanneur additif sur Qn, des résultats concernent les degrés du spanneur :
- si
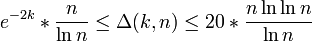
- si
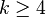
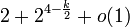
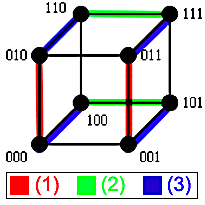
De nombreuses études sur les spanners, et des constructions pour des modèles généralisés de l'hypercube, sont dues à Arthur L. Liestman et Thomas C. Shermer. Ils ont en particulier proposé un spanner additif avec un montant 2 où les arêtes sont celles dont les extrémités
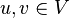
-
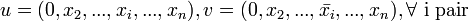

- u = (0,x2,...,xn),v = (1,x2,...,xn)
Ce processus est illustré dans l'image ci-contre où les arêtes satisfaisant une des conditions sont surlignées ; l'ensemble de ces arêtes constitue le spanner. Pour obtenir un chemin entre deux sommets, considérons que l'on démarre d'un sommet (0,x2,...,xn). On inverse d'abord ses coordonnées paires, car la condition (1) impose l'existence d'une arête sur tout sommet commençant par 0 avec une différence sur bit pair. On change ensuite la première coordonnée en 1 grâce à la condition (3), à partir de quoi on peut inverser toutes les coordonnées impaires par la condition (2). Si le sommet de destination est (1,y2,...,yn) alors on est arrivé car on commence par 1 et les coordonnées paires comme impaires ont pu être inversé ; si le sommet de destination est (0,y2,...,yn) on utilise une dernière inversion par la condition (3). Le cas où le sommet d'origine est (1,x2,...,xn) est traité de façon similaire : inverser les coordonnées impaires, passer la première coordonnée en 0, inverser les coordonnées paires, passer la première coordonnée en 1 si nécessaire. Dans l'image ci-contre, on voit le délai de 2 si on cherche un chemin de 001 à 000 : ce qui se ferait normalement directement en une étape doit se faire en trois étapes, en passant par 101 et 100.
Diffusions
Dans le problème de la diffusion (anglais broadcast), un nœud source souhaite diffuser une information à tous les autres nœuds. Dans le modèle classique, à chaque étape un nœud donné peut transmettre au plus une information, cette information utilisant une arête et étant transmise à la fin de l'étape. Dans ce modèle, la diffusion la plus performante est celle où, à chaque étape, chaque nœud en contacte un autre, c'est-à-dire que le nombre de nœuds contactés est doublé. Le nombre d'étapes minimal est donc log2n ; un graphe pouvant finir une diffusion en log2n étapes quelle que soit l'origine et en minimisant le nombre d'arêtes est un graphe de diffusion minimale (anglais minimal broadcast graph). Dans le cas où n = 2k, le nœud source doit avoir au moins k voisins car il doit diffuser à chaque étape pour faire doubler le nombre de voisins ; la source n'étant pas fixée, on obtient que chaque nœud doit avoir au moins k voisins d'où
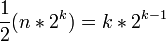

Parmi les problèmes proches se trouve le commérage (anglais gossip) où chaque nœud veut échanger une information avec tous les autres, autrement dit chaque nœud est la source d'une diffusion. Des cas particuliers s'intéressent aux variantes locales : par exemple, dans un commérage 'local', chaque nœud veut apprendre les messages de ses voisins.