Hypercube - Définition

Introduction

Une projection d'un hypercube (dans une image bi-dimensionnelle)

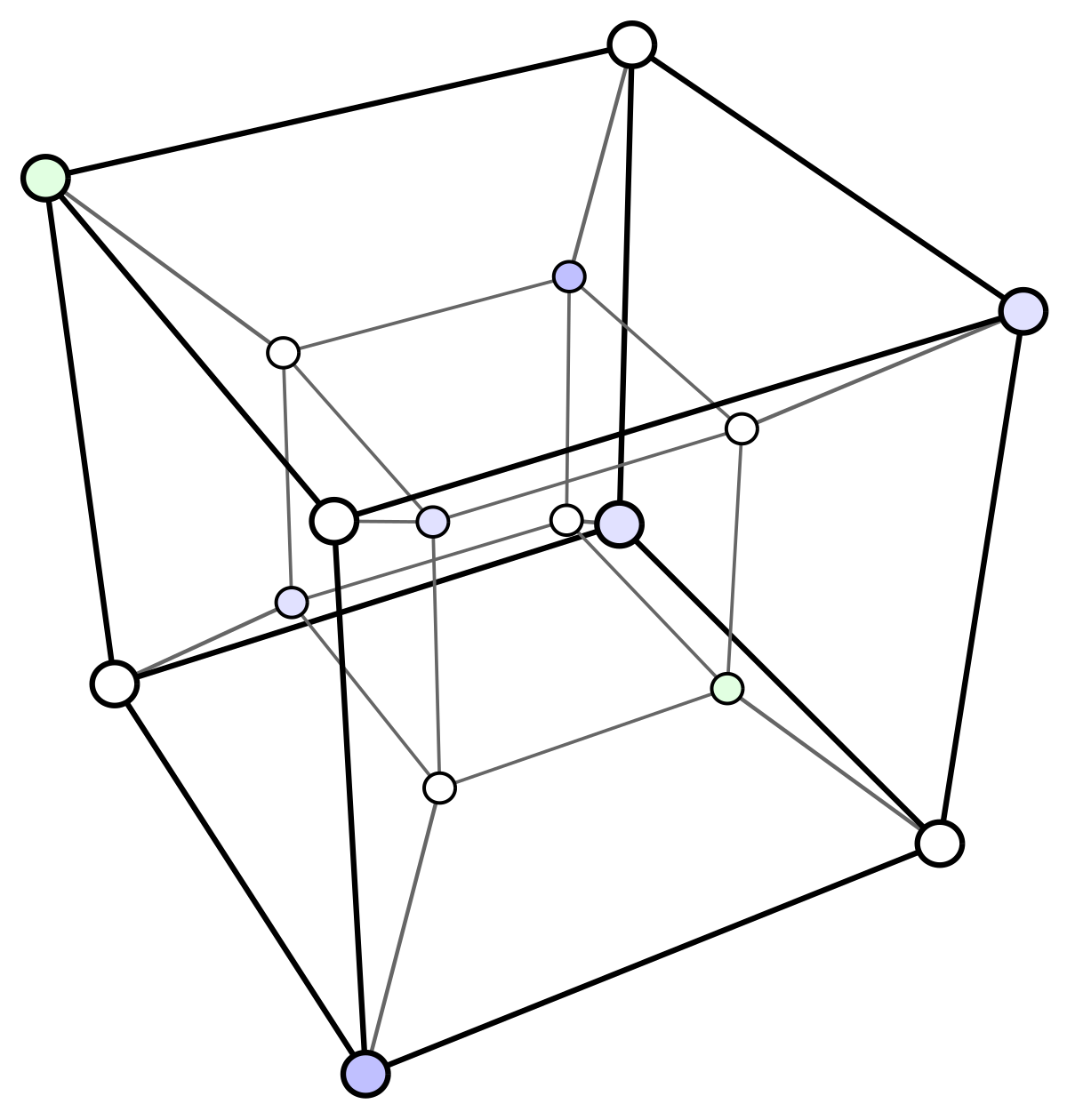
Un hypercube est, en géométrie, un analogue n-dimensionnel d'un carré (n = 2) et d'un cube (n = 3). C'est une figure fermée, compacte, convexe constituée de groupes de segments parallèles opposés alignés dans chacune des dimensions de l'espace, à angle droit les uns par rapport aux autres.

Un hypercube n-dimensionnel est aussi appelé un n-cube. Le terme « polytope de mesure » (qui est apparemment dû à Coxeter ; voir Coxeter 1973) est aussi utilisé mais il est rare. Enfin, le cas particulier du 4-cube est souvent désigné par le terme de tesseract.

Définition

Si E est un espace euclidien de dimension n muni d'une base orthonormale, on définit un hypercube unité comme l'hypervolume délimité par les 2ⁿ points dans E ayant des coordonnées égales à 0 ou 1 reliés par des segments de droite. Les hypercubes sont les figures obtenues à partir de l'hypercube unité par des similitudes.

4 dimensions

L’hypercube à quatre dimensions est également appelé tesseract en anglais, d'après Charles Howard Hinton.

D'après la formule de Gardner, on peut retrouver les propriétés du tesseract en développant (2x + 1)⁴ :

Donc l'hypercube est composé de :

• 16 sommets ;
• 32 arêtes ;
• 8 faces cubiques (soit 24 faces planes) : chacune des faces du tesseract est un cube.

L'intersection d'un hypercube avec un hyperplan donne l'équation cartésienne :

Avec les quatre coordonnées de l'hyperespace de dimension 4, à savoir x, y, z, et w. En réalité, un hyperplan en quatre dimensions peut être comparé à l'espace tridimensionnel, c’est-à-dire que l'intersection d'un hypercube avec un plan est en fait une projection 3D de cet hypercube.

• "Volume" (quadridimentionnel) : c⁴
• "Surface externe" (tridimentionnelle) : 8c³
• "Aire totale" (bidimentionnelle) : 24c²

(avec c le côté de l'hypercube)

Les faces d'un hypercube sont :

• Avant / Arrière
• Gauche / Droite
• Haut / Bas
• Ana / Kata

Représenter un hypercube de dimension n

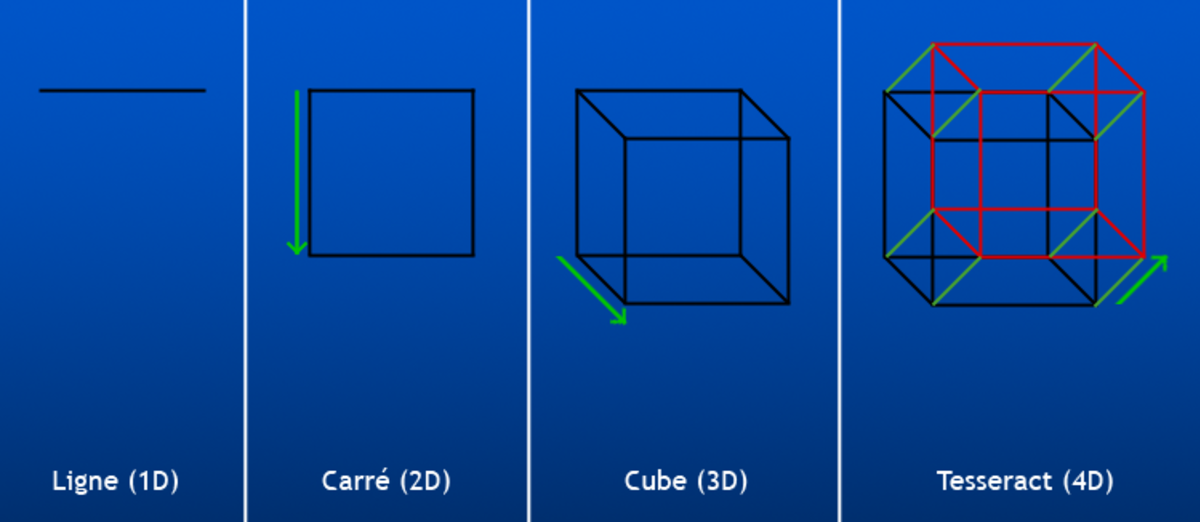
Pour représenter un hypercube de dimension n, on procède comme suit :

• Dimension 1 : Un point est un hypercube de dimension zéro. Si on déplace ce point d'une longueur unité, il balaiera un segment de droite, qui est un hypercube unité de dimension un

• Dimension 2 : Si on déplace ce segment d'une longueur unité dans une direction perpendiculaire à partir de lui-même ; il balaie un carré bi-dimensionnel.

• Dimension 3 : Si on déplace le carré d'une longueur unité dans la direction perpendiculaire à l'emplacement de celui-ci, il engendrera un cube tri-dimensionnel.

• Dimension 4 : Si on déplace le cube d'une longueur unité dans la quatrième dimension, il engendrera un hypercube unité quadri-dimensionnel (un tesseract unité).

…

• Dimension n > 3 : On trace un hypercube de dimension n-1, on reproduit son image et on lie les points deux à deux.

En résumé, la construction d'un hypercube se fait par la translation du cube de dimension inférieure selon un axe perpendiculaire aux dimensions de ce cube.

Chaque nouvelle dimension est perpendiculaire aux précédentes

Les hypercubes sont une des quelques familles de polytopes réguliers qui sont représentés dans un nombre quelconque de dimensions. Le polytope dual d'un hypercube est appelé un polytope croisé. le 1-squelette d'un hypercube est un graphe hypercube.

Une généralisation du cube aux dimensions plus grandes que trois est appelée un « hypercube », « n-cube » ou « polytope mesure ». Le tesseract est l'hypercube quadri-dimensionnel ou 4-cube. C'est un polytope régulier. C'est aussi un cas particulier de parallélotope : un hypercube est un parallélotope droit dont les arêtes sont de même longueur.

Le patron d’un hypercube.