Hyperthermie magnétique - Définition

Influence de la taille de nanoparticules sur leur structure en domaines

La taille de nanoparticules a une forte influence sur leur structures en domaines. Les plus petites particules sont composées d'un seul domaine (mono-domaines). Les plus grosses ont plusieurs domaines leur permettant de minimiser leur énergie magnétostatique. Pour des tailles intermédiaires, elles présentent une belle structure tourbillonaire appelée vortex. En première approximation, on peut considérer qu'une nanoparticule n'est plus monodomaine lorsque sa taille excède celle d'une paroi de domaine dans le matériau. Cette taille varie de quelques nanomètres à quelques centaines de nanomètres, suivant les matériaux. La structure en domaine des nanoparticules a une forte influence sur le mécanismes de leur renversement d'aimantation, sur leur cycle d'hystérésis, et donc sur leur propriétés d'hyperthermie.

Mécanismes impliqués dans l'aimantation de nanoparticules multi-domaines

Dans des particules multi-domaines, les ingrédients pour décrire le renversement d'aimantation sont la nucléation de nouveaux domaines et la propagation de parois de domaines. Ces deux mécanismes sont fortement influencés par les défauts structuraux à la surface ou à l'intérieur des nanoparticules, ce qui rend difficile les prédictions quantitatives de la forme et de l'aire des cycles d'hystérésis à partir de paramètres intrinsèques des nanoparticules.

Modèles utilisables pour les particules monodomaines

Certains modèles permettent de calculer les propriétés et l'aire du cycle d'hystérésis dans des cas particuliers.

Le modèle de réponse linéaire

Le modèle de réponse linéaire est uniquement valide quand la réponse du matériau magnétique est linéaire en fonction du champ magnétique appliqué, et peut donc s'écrire sous la forme M = χH, où χ est la susceptibilité complexe du matériau. Il est donc seulement valide quand le champ magnétique appliqué est beaucoup plus petit que le champ magnétique nécessaire pour saturer l'aimantation de la nanoparticule. Ce modèle prend en compte la relaxation de Néel et la relaxation de Brown. Il utilise pour cela un temps de relaxation moyen τ, donné par . La composante hors-phase de l'aimantation est alors donnée par . Le retard entre le champ magnétique et l'aimantation donne alors lieu à un cycle d'hystérésis de forme elliptique et d'aire A = πμ₀H²χ''.

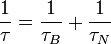
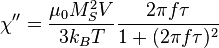
Le modèle de Stoner-Wohlfarth et l'aire maximale

Le modèle de Stoner-Wohlfarth permet de calculer le cycle d'hystérésis de nanoparticules magnétiques pour T=0 en supposant que les particules sont immobiles dans le champ magnétique (le mouvement brownien est donc négligé) et sans interaction magnétique. Son intérêt est de prédire "l'aire maximale" pour des particules indépendantes ayant des propriétés données. En effet, l'énergie thermique ou le mouvement brownien ne peuvent que diminuer l'aire du cycle d'hystérésis (voir plus loin).
Le modèle de Stoner-Wohlfarth prédit que le champ coercitif pour T=0 d'une assemblée de nanoparticules ayant des axes d'anisotropie orientés aléatoirement dans l'espace est donné par , et que l'aire du cycle d'hystérésis est approximativement A = 2μ₀M_SH_C(0).

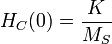
Extensions du modèle de Stoner-Wohlfarth pour prendre en compte la tempéature et la fréquence

Des extensions du modèle de Stoner-Wohlfarth ont été réalisées afin d'inclure l'effet de la température et de la fréquence sur le cycle d'hystérésis. Ces extensions ne sont valides que quand l'effet de la temperature et de la fréquence sont faibles c'est-à-dire lorsque f > > 1 / τ_N. Des simulations numériques ont montré que, dans ce cas, l'expression du champ coercitif pour des nanoparticules orientées de manière aléatoire devient . On peut voir d'après cette expression que l'effet de la temperature est de réduire le champ coercitif des nanoparticules.