Inégalité FKG - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L’inégalité FKG, due à Fortuin, Kasteleyn et Ginibre est une version généralisée de l'inégalité de Tchebychev pour les sommes. C'est une inégalité de corrélation utilisée, par exemple, en théorie de la percolation, et dans l'étude du modèle de graphes aléatoires dû à Erdős et Rényi.
Énoncé
Sous la forme due à Harris, l'inégalité FKG concerne un ensemble fini ou dénombrable J dont chaque élément j est soit dans l'état 0, avec probabilité 1-p, soit dans l'état 1 avec probabilité p. L'état global du système J est donc décrit par un élément de
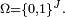
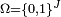
Inégalité FKG —
- Soit deux variables aléatoires X et Y croissantes sur
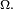
![\mathbb{E}\left[XY\right] \geq \mathbb{E}\left[X\right] \mathbb{E}\left[Y\right].\,](https://static.techno-science.net/illustration/Definitions/autres/f/f672fb83c11739ffdbc47d38d4f90137_6519337e8488d6232754a1535efee766.png)
- Soit deux parties croissantes A et B de
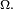
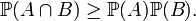
Cela revient à dire qu'il y a une corrélation positive entre les variables concernées, puisqu'on peut reformuler la première inégalité sous la forme
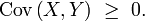
- Le deuxième point de l'inégalité FKG est obtenu comme conséquence immédiate du premier point, en spécialisant au cas particulier où X est la fonction indicatrice de A et où Y est la fonction indicatrice de B.
- L'inégalité vaut aussi pour des variables ou des parties décroissantes, mais le sens des inégalités change lorsque les variables ou les parties concernées ont des sens de monotonie opposés.
- Il y a des formes plus générales de l'inégalité FKG, avec les mêmes conclusions, mais pour des espaces produits plus généraux, munis d'une mesure qui n'est pas nécessairement une mesure produit (voir FKG inequality).
Ordre et croissance
- On définit une relation d'ordre partielle sur Ω comme suit : pour
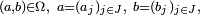
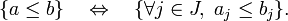
- Si on identifie Ω à l'ensemble des parties de J, la relation d'ordre ci-dessus s'interprète comme la relation d'inclusion. Ce parallèle ne tient plus si l'on veut généraliser de
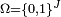
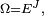
- Comme d'ordinaire, une application X définie sur Ω, à valeurs réelles, est dite croissante si
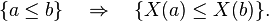
- Une partie A de Ω est dite croissante si
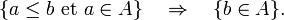
- De manière équivalente, une partie A de Ω est dite croissante si sa fonction indicatrice est croissante.
- La propriété de décroissance d'une application ou d'une partie a une définition analogue.
- Percolation : J est l'ensemble des arêtes du réseau
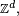
- l'ensemble A des configurations possédant un amas infini est croissant (on dit que la propriété d'existence d'un amas infini est croissante) ;
- pour deux sites donnés, x et y, la propriété "x est relié à y" est croissante ;
- la propriété "x appartient à un amas infini" est croissante.
- Modèle d'Erdős-Rényi : J est l'ensemble des n(n-1)/2 arêtes potentielles entre n sommets numérotés de 1 à n, arêtes présentes avec probabilité p et absentes avec probabilité 1-p, indépendamment les unes des autres. L'ensemble des arêtes présentes définit un graphe aléatoire, noté G(n,p), dont Erdős et Rényi ont étudié certaines propriétés (évènements) et certains paramètres (variables aléatoires). Parmi ces propriétés et paramètres,
- la connexité est croissante ;
- la planarité est décroissante ;
- le nombre chromatique est croissant ;
- la taille de l'ensemble indépendant de taille maximale (independence number) est décroissante ;
- la propriété triangle-free est décroissante.

















































