Inégalité FKG - Définition
La liste des auteurs de cet article est disponible ici.
Preuve
Inégalité de corrélation
Modulo des hypothèses d'intégrabilité, dans le cas où l'espace de départ est muni d'une relation d'ordre totale, on a les inégalités suivantes :
Inégalité de corrélation —
- Soit deux variables aléatoires réelles X et Y définies et croissantes sur un ensemble
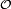
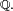
![\mathbb{E}\left[XY\right] \geq \mathbb{E}\left[X\right] \mathbb{E}\left[Y\right].\,](https://static.techno-science.net/illustration/Definitions/autres/f/f672fb83c11739ffdbc47d38d4f90137_6519337e8488d6232754a1535efee766.png)
- Soit Z une variable aléatoire réelle définie sur un ensemble
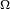
![\mathbb{E}\left[f(Z)g(Z)\right] \geq \mathbb{E}\left[f(Z)\right] \mathbb{E}\left[g(Z)\right].\,](https://static.techno-science.net/illustration/Definitions/autres/6/68deb224f1ea524c7ec9756a3bad4ffd_0df855f66ff4b0ffeacb0423209c0542.png)
- On considère l'espace produit
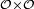
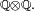
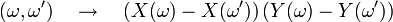
- est positive ou nulle sur
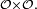
![\begin{align} 0 &\le \int_{\mathcal{O}\times\mathcal{O}}\ (X(\omega)-X(\omega^{\prime})(Y(\omega)-Y(\omega^{\prime})\ \mathbb{Q}\otimes\mathbb{Q}(d\omega,d\omega^{\prime}) \\ &= \int_{\mathcal{O}\times\mathcal{O}}\ [X(\omega)Y(\omega)+X(\omega^{\prime})Y(\omega^{\prime})-X(\omega)Y(\omega^{\prime})-X(\omega^{\prime})Y(\omega)]\ \mathbb{Q}\otimes\mathbb{Q}(d\omega,d\omega^{\prime}) \\ &=2\ \mathbb{E}\left[XY\right]-2\ \mathbb{E}\left[X\right] \mathbb{E}\left[Y\right], \end{align}](https://static.techno-science.net/illustration/Definitions/autres/5/59e7fc94ee66c9966c8a5d36f1b411f5_f44c0a4c737577e43b300a0ec5306b68.png)
- où la première inégalité découle de la croissance de l'intégrale par rapport à une mesure. La dernière égalité provient de la linéarité de l'intégrale, et du Théorème de Fubini appliqué aux quatre intégrales obtenues à l'aide de la linéarité.
- La deuxième inégalité est une conséquence de la première, en spécialisant à
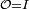
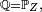
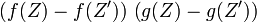
- est positive ou nulle sur
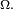
![\begin{align} 0 &\le \mathbb{E}\left[\left(f(Z)-f(Z^{\prime}\right)\,\left(g(Z)-g(Z^{\prime}\right)\right] \\ &=\mathbb{E}\left[f(Z)g(Z)\right]+\mathbb{E}\left[f(Z^{\prime})g(Z^{\prime})\right]-\ \mathbb{E}\left[f(Z^{\prime})g(Z)\right]-\mathbb{E}\left[f(Z)g(Z^{\prime})\right] \\ &=2\ \mathbb{E}\left[f(Z)g(Z)\right]-\ \mathbb{E}\left[f(Z^{\prime})\right] \mathbb{E}\left[g(Z)\right]-\mathbb{E}\left[f(Z)\right] \mathbb{E}\left[g(Z^{\prime})\right] \\ &=2\ \mathbb{E}\left[f(Z)g(Z)\right]-\ 2\mathbb{E}\left[f(Z)\right] \mathbb{E}\left[g(Z)\right], \end{align}](https://static.techno-science.net/illustration/Definitions/autres/5/51fc045ff9a74276a5e731e6aae936ad_6eb3b703a80c9b95e7acdd5a439abee8.png)
- où on a utilisé à plusieurs reprises l'indépendance des deux variables Z et Z', et l'identité en loi de ces deux variables.
Là encore, on peut reformuler la deuxième inégalité sous la forme
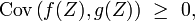
et là encore, on peut changer le sens de monotonie d'une ou deux des variables ou fonctions concernées, quitte éventuellement à changer le sens de l'inégalité.
L'inégalité de Tchebychev pour les sommes est une conséquence immédiate de l'inégalité de corrélation ci-dessus : il suffit de considérer le cas particulier où la variable aléatoire réelle Z suit la loi uniforme discrète sur
![\scriptstyle\ [\![1,n]\!].\](https://static.techno-science.net/illustration/Definitions/autres/c/cc957f4699e32287bf3fa138b22712b6_8d5fcd8df44d8639510311dc89f6a959.png)
Cas fini
On fait la démonstration dans le cas général où l'état global du système fini J est décrit par un élément
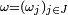
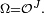
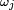
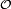
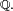
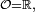
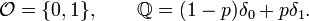
Le résultat démontré ici est donc (du moins dans le cas où J est fini) plus fort que l'inégalité FKG annoncée.
On suppose, sans perte de généralité, que
![\scriptstyle\ J=[\![1,n]\!],\](https://static.techno-science.net/illustration/Definitions/autres/2/2a1399f4c1f728b34c1f2f50ed63acc3_d2402079a1fc4150b10cd5be411a757f.png)
On note
![\begin{align} \widehat{X}(\omega_{n}) &=\int_{\mathcal{O}^{n-1}}\ X(\omega)\ \mathbb{Q}(d\omega_{1})\dots\mathbb{Q}(d\omega_{n-1}) \\ &=\mathbb{E}\left[X\left|\omega_{n}\right.\right] \end{align}](https://static.techno-science.net/illustration/Definitions/autres/7/7271b6660567f096870cb6ffee75cbad_f9c1cb3cf629987afd160596c1c1ce10.png)
l'espérance conditionnelle de X sachant la n-ème coordonnée

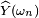
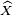
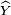
![\mathbb{E}\left[\widehat{X}\widehat{Y}\right] \geq \mathbb{E}\left[\widehat{X}\right] \mathbb{E}\left[\widehat{X}\right].\,](https://static.techno-science.net/illustration/Definitions/autres/f/fefd9389cf894d5414b5ebf710e89e40_2d82e9b5e447340fa9b83420ac8a2044.png)
D'autre part, par propriété de l'espérance conditionnelle (ou, dans ce cas particulier, à cause du théorème de Fubini),
![\begin{align} \mathbb{E}\left[\widehat{X}\right] \mathbb{E}\left[\widehat{Y}\right] &= \mathbb{E}\left[\mathbb{E}\left[X\left|\omega_{n}\right.\right]\right]\ \mathbb{E}\left[\mathbb{E}\left[Y\left|\omega_{n}\right.\right]\right] \\ &= \mathbb{E}\left[X\right] \mathbb{E}\left[Y\right]. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/3/36b08ee683b89fb59562fd4e756347a1_94527ed5069b9313283812ae889c7ee2.png)
Considérons maintenant que la n-ème coordonnée

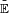
![\begin{align} \tilde{\mathbb{E}}\left[Z\right] &=\int_{\mathcal{O}^{n-1}}\ Z(\omega)\ \mathbb{Q}(d\omega_{1})\dots\mathbb{Q}(d\omega_{n-1}). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/0/0ba6c20b6b3a5d4dd87720e68046ee4d_9f1b2e42e99b7820fbf6e8cc9cdc5b1a.png)
On considère les applications
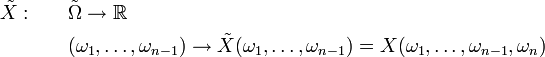
et
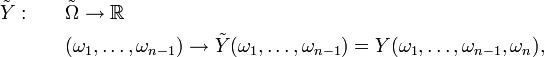
qui sont croissantes sur
![\tilde{\mathbb{E}}\left[\tilde{X}\right]=\widehat{X}(\omega_{n}) =\mathbb{E}\left[X\left|\omega_{n}\right.\right],](https://static.techno-science.net/illustration/Definitions/autres/9/92bf8677d2f30779d60235bfd09633b5_74aa3587019e66918cef154c52fdf2d8.png)
![\tilde{\mathbb{E}}\left[\tilde{Y}\right]=\widehat{Y}(\omega_{n}) =\mathbb{E}\left[Y\left|\omega_{n}\right.\right].](https://static.techno-science.net/illustration/Definitions/autres/9/98ca39d1d1b1e7bdbafcb65ca8d65dfc_57ee0200997b4b552909884bef92a500.png)
On a donc en vertu de l'hypothèse de récurrence (rang n-1)
![\mathbb{E}\left[XY\left|\omega_{n}\right.\right]=\tilde{\mathbb{E}}\left[\tilde{X}\tilde{Y}\right]\ge\tilde{\mathbb{E}}\left[\tilde{X}\right]\tilde{\mathbb{E}}\left[\tilde{Y}\right]=\widehat{X}(\omega_{n})\widehat{Y}(\omega_{n}).](https://static.techno-science.net/illustration/Definitions/autres/a/af16a2b15bb1285455623d4ace3f514f_76079a85665fa121f3c2b786a3e0a4a5.png)
Finalement, avec la première inégalité,
![\mathbb{E}\left[XY\right]=\mathbb{E}\left[\mathbb{E}\left[XY\left|\omega_{n}\right.\right]\right]\ge\mathbb{E}\left[\widehat{X}\widehat{Y}\right]\ge\mathbb{E}\left[X\right]\mathbb{E}\left[Y\right].](https://static.techno-science.net/illustration/Definitions/autres/8/8002886c11357afcf6ecacdc92f95d06_e3b3868c44cdaf943d3c9a3562212a74.png)
A ce stade on a démontré l'inégalité FKG utile au modèle d'Erdos-Renyi, mais on n'a pas encore une inégalité FKG suffisamment puissante pour la théorie de la percolation. C'est l'objet de la section suivante.
Cas infini dénombrable
La démonstration se fait à partir du cas fini, par passage à la limite, en utilisant un théorème de convergence presque sûre pour les martingales à carré intégrable. Voir Grimmett "Percolation", page 36, section 2.2.

















































