Intégrale de chemin - Définition
La liste des auteurs de cet article est disponible ici.
Expression du propagateur en termes d'intégrale de chemin
Cherchons l'expression du propagateur
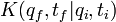

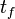
Application de l'équation de Chapman-Kolmogorov
On découpe l'intervalle de temps
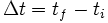
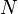

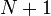
|
|
avec
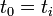
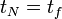
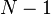
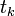
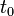
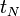
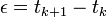
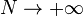
L'application de l'équation de Chapman-Kolmogorov une première fois permet d'écrire :
|
|
puis, en l'appliquant une deuxième fois :
|
|
et ainsi de suite. On obtient au final après
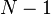
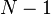
![K(q_N,t_N|q_0,t_0) \ = \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ K(q_N,t_N|q_{N-1},t_{N-1}) \times \dots \times K(q_{k+1},t_{k+1}|q_{k},t_{k}) \times \dots \times K(q_{1},t_{1}|q_0,t_0)](https://static.techno-science.net/illustration/Definitions/autres/d/d525ac09f5944c10cacd8c1969dc1628_af0f5ad616416d0594a7193b076d9329.png)
|
On est ainsi amené à considérer le propagateur élémentaire :
 |
Propagateur élémentaire : formule de Feynman-Dirac
Pour une particule de masse
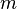
|
|
et le propagateur élémentaire s'écrit :
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) \ = \ < q_{k+1} |e^{-i \, [ \, \hat{H}_0 + V(\hat{q}) \, ] \, \epsilon /\hbar} | q_k >](https://upload.wikimedia.org/math/7/9/9/79913cbea2dd47ca49c3d2bf6a19afd6.png) |
On utilise la formule de Trotter-Kato :
|
|
Cette formule n'est pas triviale, car les opérateurs
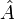
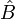
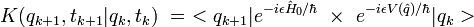 |
On peut sortir l'exponentielle contenant le potentiel qui ne dépend que de la position :
 |
L'élément de matrice restant est le propagateur de la particule libre, donc on peut finalement écrire l'expression :
|
|
Or l'expression du propagateur libre est connue exactement :
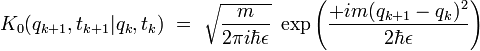
|
On remarque que l'argument de l'exponentielle peut se réécrire en termes d'une expression discrètisée de la vitesse :
|
|
comme :
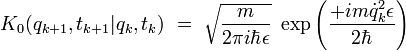
|
On en déduit que le propagateur élémentaire s'écrit :
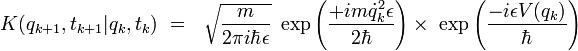
|
Les arguments des deux exponentielles étant maintenant des nombres complexes, on peut écrire sans difficultés :
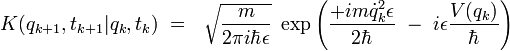
|
soit encore :
|
|
Le terme entre parenthèse représente le Lagrangien de la particule :
|
|
d'où la formule de Feynman-Dirac pour le propagateur élémentaire :
|
|
Intégrale de chemin
On injecte l'expression de Feynman-Dirac dans la formule générale :
![K(q_N,t_N|q_0,t_0) \ = \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ K(q_N,t_N|q_{N-1},t_{N-1}) \times \dots \times K(q_{k+1},t_{k+1}|q_{k},t_{k}) \times \dots \times K(q_{1},t_{1}|q_0,t_0)](https://static.techno-science.net/illustration/Definitions/autres/d/d525ac09f5944c10cacd8c1969dc1628_af0f5ad616416d0594a7193b076d9329.png)
|
Il vient :
|
|
L'argument des exponentielles étant des nombres complexes, on peut écrire :
|
|
On reconnait dans l'argument de l'exponentielle une discrétisation de l'action classique :
![\lim_{N\to\infty} \sum_{k=1}^{N-1} L(q_k,\dot{q}_k) \epsilon \ = \ \int_{t_0}^{t_N} L(q(t),\dot{q}(t)) dt \ = \ S \left[ \, q(t) \, \right]](https://static.techno-science.net/illustration/Definitions/autres/f/f9528674af5aeaf41cbd5441eb7d1203_ae79d9e72264ada78e481fbb28eae586.png)
|
On en déduit avec Feynman l'expression du propagateur comme intégrale fonctionnelle sur tous les chemins continus :
avec la mesure formelle :
![\mathcal{D}q(t) \ = \ \lim_{N\to\infty} \left( \, \frac{m}{2 \pi i \hbar \epsilon} \, \right)^{N/2} \ \left[ \, \prod_{k=1}^{N-1} dq_k \, \right]](https://static.techno-science.net/illustration/Definitions/autres/4/4673b2ac26a7fc1248cb2842e76d3746_1e454568353e7a99ff489162792ed4e4.png)
|
Interprétation
La formule de Feynman :
|
|
admet l'interprétation suivante : pour calculer l'amplitude de transition du point initial
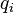

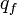
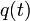
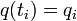
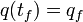
![\exp ( i S[q(t)]/\hbar )\,](https://static.techno-science.net/illustration/Definitions/autres/d/dd1e01dee08cad29a0c1208abd9811ed_2bf84bfc53debd12c42716481c213297.png)
![S[q(t)]\,](https://static.techno-science.net/illustration/Definitions/autres/0/0e9fd62e69c48d17f5295b0c4d75f7a8_fd7fdda57ed357281fd4b239e417826f.png)
Cette interprétation est l'œuvre de Feynman seul, Dirac n'ayant pas franchi le pas. Elle est implicite dans sa thèse de 1942, et explicite dans la publication de 1948.

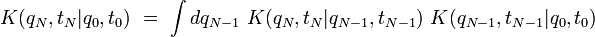
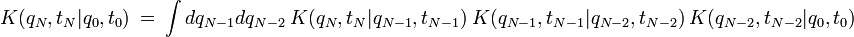
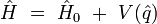
![e^{t(\hat{A} + \hat{B})} \ = \ \lim_{n \to \infty} \ \left[ \ e^{\hat{A}t/n} \ \times \ e^{\hat{B}t/n} \ \right]^n](https://static.techno-science.net/illustration/Definitions/autres/6/6a7af09d6c118d00474c31ca24a8276d_52139f9a26e2a4e5e3c9de1012803afa.png)
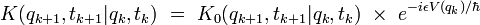
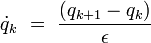
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) \ = \ \ \sqrt{\frac{m}{2 \pi i \hbar \epsilon}} \ \exp \left[ + \frac{i}{\hbar} \ \left( \frac{m}{2} \dot{q}_k^2 \ - \ V(q_k) \right) \ \epsilon \ \right]](https://static.techno-science.net/illustration/Definitions/autres/d/d2e6c64d9a6b0993d7984a6756c4d2a8_fe6c56d6b4987a6ff8d0687676279faf.png)
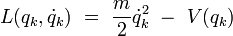
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) \ = \ \ \sqrt{\frac{m}{2 \pi i \hbar \epsilon}} \ \exp \left[ + \frac{i}{\hbar} \ L(q_k,\dot{q}_k) \ \epsilon \ \right]](https://static.techno-science.net/illustration/Definitions/autres/4/4dac735213dbe66e97e99cd56ce05dee_ce429ae8e62d8ec0258d805f5b2cda82.png)
![K(q_N,t_N|q_0,t_0) \ = \ \left( \, \frac{m}{2 \pi i \hbar \epsilon} \, \right)^{N/2} \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ \exp \left[ + \frac{i}{\hbar} \ L(q_{N-1},\dot{q}_{N-1}) \ \epsilon \ \right] \times \dots \times \exp \left[ + \frac{i}{\hbar} \ L(q_k,\dot{q}_k) \ \epsilon \ \right] \times \dots \times \exp \left[ + \frac{i}{\hbar} \ L(q_0,\dot{q}_0) \ \epsilon \ \right]](https://static.techno-science.net/illustration/Definitions/autres/1/1958e35f000c6df83210aedf460d91a7_4890cc3c7fcbd52001c91478dfa12548.png)
![K(q_N,t_N|q_0,t_0) \ = \ \left( \, \frac{m}{2 \pi i \hbar \epsilon} \, \right)^{N/2} \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ \exp \left[ + \frac{i}{\hbar} \ \left[ \, L(q_{N-1},\dot{q}_{N-1}) + \dots + L(q_k,\dot{q}_k) + \dots + L(q_0,\dot{q}_0) \, \right] \ \epsilon \ \right]](https://static.techno-science.net/illustration/Definitions/autres/6/63a8e31f7a4b036d75d0d1387c09b498_015ce49ba338fbf7abaf87aec2de6c22.png)
![K(q_f,t_f|q_i,t_i) \ = \ \int \mathcal{D}q(t) \ \textrm{e}^{ + \frac{i \, S \left[ \, q(t) \, \right]}{\hbar}}](https://static.techno-science.net/illustration/Definitions/autres/c/c44fe6f004a074e716d66ac3cf21b97c_8d66d9c87e4175240bca10e4f85e5773.png)

















































