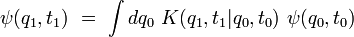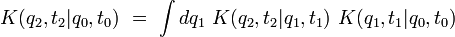Intégrale de chemin - Définition

Rappels sur le propagateur de l'équation de Schrödinger

Pour simplifier les notations, on se restreint ci-dessous au cas d'une seule dimension d'espace. Les résultats s'étendent sans difficulté à un nombre quelconque de dimensions.

Définition

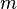
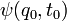
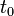
Considérons une particule de masse non relativiste, décrite en mécanique quantique par une fonction d'onde. Supposons que l'on se donne la condition initiale à un instant initial fixé. Alors, la fonction d'onde à un instant ultérieur , solution de l'équation de Schrödinger, est donnée par l'équation intégrale :

où est le propagateur de la particule :

est l'opérateur hamiltonien de la particule.

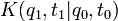
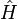
Équation de Chapman-Kolmogorov

Rappelons que, si , le propagateur obéit à l'équation de Chapman-Kolmogorov :

Cette relation va nous permettre de trouver l'expression du propagateur en termes d'une intégrale de chemin.

Bibliographie

Textes historiques

• Richard P. Feynman ; The principle of least action in quantum mechanics, thèse de l'université de Princeton. Cette thèse vient d'être publiée par Laurie M. Brown (cf. ci-dessous).

• Richard P. Feynman ; Space-time approach to non-relativistic quantum mechanics, Review of Modern Physics 20 (1948) 267. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) .

• PAM Dirac ; The lagrangian in quantum mechanics, Physikalische Zeitschrift der Sowjetunion 3(1) (1932) 64. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) .

• Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),. Contient la thèse originale de Feynman, ainsi que les deux articles précédents.

Ouvrages de références

• Jean Zinn-Justin ; Intégrale de chemin en mécanique quantique : Introduction, Collection savoirs actuels, E.D.P. Sciences/C.N.R.S. Editions (2003), . Excellente introduction au sujet, ce livre est le fruit de nombreuses années d'enseignement au Magistère Interuniversiataire de Physique de l'E.N.S.
• Claude Cohen-Tannoudji ; Compléments de mécanique quantique, (1966). Cours donné en 1966 par le prix Nobel 1997 (Collège de France, Paris). Aborde la formulation Lagrangienne de la mécanique quantique, et l'utilisation des fonctions de Green. Notes de cours rédigées en 1966 par Serge Haroche (Collège de France, Paris).
• Richard P. Feynman and André R. Hibbs, Quantum Mechanics and Path Integrals, New York: McGraw-Hill (1965), .
• Larry S. Schulman ; Techniques & Applications of Path Integration, Jonh Wiley & Sons (New York-1981), ISBN . Réédité par Dover Publications, Inc. (2005), . Une autre référence, un peu plus moderne que la précédente.
• Christian Grosche & Frank Steiner; Handbook of Feynman Path Integrals, Springer Tracts in Modern Physics 145, Springer-Verlag (1998), .
• Philippe A. Martin ; L'intégrale fonctionnelle ; Presses Polytechniques Universitaires Romandes (1996), .
• Lundqvist & co ; Path Summation ; World scientific (1988), .
• Martin Veltman ; Diagrammatica, CambridgeLNP
• Lewis H. Ryder ; Quantum Field Theory (Cambridge University Press, 1985), .
• R.J. Rivers ; Path Integrals Methods in Quantum Field Theory, Cambridge University Press (1987), .
• Hagen Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2004), . (Disponible aussi en ligne au format pdf).
• Christian Grosche  ; An introduction into the Feynman path integral, cours donné au Quantenfeldtheorie und deren Anwendung in der Elementarteilchen- und Festkörperphysik, Universität Leipzig, 16-26 November 1992. Texte complet disponible sur l'ArXiv : hep-th/9302097.
• Sanjeev Seahra ; Path Integrals in Quantum Field Theory, notes du cours Quantum Field Theory donné en 2000 par Eric Poisson à l'University of Waterloo (Canada). Texte complet disponible au format pdf.
• Richard MacKenzie ; Path integral methods and applications, cours donné aux Rencontres du Vietnam: VIth Vietnam School of Physics, Vung Tau, Vietnam, 27 December 1999 - 8 January 2000. Texte complet disponible sur l'ArXiv : quant-ph/0004090.
• Gert Roepstorff ; Path Integral Approach to Quantum Physics, Springer-Verlag (1994), .

Approche mathématiquement rigoureuse

• S. Albeverio & R. Hoegh-Krohn. ; Mathematical Theory of Feynman Path Integral, Lecture Notes in Mathematics 523, Springer-Verlag (1976), ISBN .
• James Glimm et Arthur Jaffe Quantum Physics: a Functional Integral Point of View, New York: Springer-Verlag (1981), .
• Gerald W. Johnson and Michel L. Lapidus ; The Feynman Integral and Feynman's Operational Calculus, Oxford Mathematical Monographs, Oxford University Press (2002), .
• Etingof, Pavel ; Geometry and Quantum Field Theory, M.I.T. OpenCourseWare (2002). Ce cours en ligne, conçu pour les mathématiciens, est une introduction rigoureuse à la théorie quantique des champs via les intégrales fonctionnelles.
• Cécile DeWitt-Morette ; Feynman's path integral - Definition without limiting procedure, Communication in Mathematical Physics 28(1) (1972) pp. 47–67. Texte complet disponible sur : Euclide Project.
• Pierre Cartier & Cécile DeWitt-Morette ; A new perspective on functional integration, Journal of Mathematical Physics 36 (1995) pp. 2137-2340. Texte complet disponible sur l'ArXiv : funct-an/9602005.
• Pierre Cartier ; L'intégrale de chemin de Feynman : d'une vue intuitive à un cadre rigoureux, dans : Leçons de mathématiques d'aujourd'hui, Collection Le sel et le fer, Cassini (2000) pp.27-59 .
• Alain Connes & Dirk Kreimer : Communication in Mathematical Physics 210 (2000)1. 249-273
• Alain Connes & Marcolli : Communication in Mathematical Physics 216 (2001),1, 215-241
• Alain Connes ; page personnelle, articles 137, 148, 155, 157, 158, 162, 165, 167.