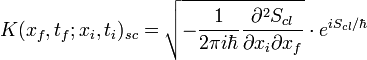Intégrale de chemin - Définition
La liste des auteurs de cet article est disponible ici.
Limite semi-classique
Dans la limite où l'action du système est beaucoup plus grande que

Considérons un Lagrangien standard:
![\mathcal{L}[x,\dot{x}]= \frac{m\dot{x}^{2}}{2}- V(x)](https://static.techno-science.net/illustration/Definitions/autres/a/aabc30b9b9f82daf69db73f1f376c7c4_600cf07dbee8eeeec488c39f78c49e6d.png)
On écrit alors l'action sous la forme suivante, en se limitant au deuxième ordre:
![S[x] \approx S[x_{c}]+ \int_{t_{i}}^{t_{f}}dt \underbrace{\frac{\delta S}{\delta x(t)}|_{x_{c}}}_{=0} y(t) + \frac{1}{2} \int_{t_{i}}^{t_{f}}dt_{1} dt_{2} \frac{\delta^{2} S}{\delta x(t_{1})\delta x(t_{2}) }|_{x_{c}}y(t_{1})y(t_{2})\Longrightarrow](https://static.techno-science.net/illustration/Definitions/autres/a/a2af42c15acf496b8eb59cbf9e0fcc11_53b5f9ee46a2163604b3fa44e51d34df.png)
![S[x]\approx S[x_{c}]+ \frac{1}{2} \int_{t_{i}}^{t_{f}}dt (m \dot{y}^{2} - V''(x_{c}) y^{2})](https://static.techno-science.net/illustration/Definitions/autres/3/31659c3c8a96ea1bff7209fd7974bdb8_5a758c67d500206f93c1f8ab18923fc1.png)
on peut donc approximer le propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) \approx e^{i S[x_{c}]/ \hbar} \int \mathcal{D}[y] e^{i \int_{t_{i}}^{t_{f}}dt (m \dot{y}^{2} - V''(x_{c}) y^{2})/2\hbar}](https://static.techno-science.net/illustration/Definitions/autres/3/34a01a003d70ba5737366c55bdc21769_7d74622c4899795ba4393f2fefcac10f.png)
une intégration par partie de l'exposant ramène à une forme Gaussienne:
![K(x_{f},t_{f};x_{i},t_{i})\approx e^{i S[x_{c}]/ \hbar} \int \mathcal{D}[y] e^{i \int_{t_{i}}^{t_{f}}dt (y[-m \frac{d^{2}}{dt^{2}} - V''(x_{c}] y)/2\hbar}](https://static.techno-science.net/illustration/Definitions/autres/2/2922ad0fcf82f997d7c301df4ff54768_b0ca9670d46774cf13ccda2060229343.png)
Définissons l'opérateur
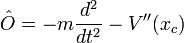
les règles de calcul des intégrales Gaussiennes fournissent:
![K(x_{f},t_{f};x_{i},t_{i}) \approx cste \cdot \sqrt{\frac{1}{Det (\hat{O})}}\cdot e^{i S[x_{c}]/ \hbar}](https://static.techno-science.net/illustration/Definitions/autres/6/670ad65fe69c000b2c03ba8e2ee198cf_a284ad8c62584fd07bcec4d997b3a3c5.png)
Considérons maintenant la fonction Ψ(t) définie comme suit:
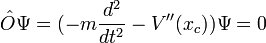
avec les conditions de bords:
Ψ(ti) = 0
Ψ'(ti) = 1
On peut alors montrer que:
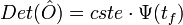
ce qui nous donne pour l'approximation du propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) \approx \sqrt{\frac{A}{\Psi(t_{f})}}\cdot e^{i S[x_{c}]/ \hbar}](https://static.techno-science.net/illustration/Definitions/autres/c/cf282603976ee6a16a78d82e308ab3ce_f45a7fd6578bf79f680b009202186c83.png)
on détermine la constante A à partir du propagateur de la particule libre:
![K_{fp}(x_{f},t_{f};x_{i},t_{i})=\sqrt{\frac{m}{2\pi i \hbar (t_{f}-t_{i})}} e^{i S[x_{c}]/ \hbar}](https://static.techno-science.net/illustration/Definitions/autres/5/58aedadc4a116db583b15d5e1960c58f_391f12549ef3149ecb58067abff47845.png)
dans le cas de la particule libre, la fonction Ψ qui satisfait les conditions exposées plus haut est Ψ(t) = t − ti, ce qui nous donne immédiatement une expression pour A. On obtient finalement l'approximation dite semi-classique du propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) \approx \sqrt{\frac{m}{2 \pi i \hbar \Psi(t_{f})}}\cdot e^{i S[x_{c}]/ \hbar}](https://static.techno-science.net/illustration/Definitions/autres/a/a400c660a68b8b9d59da52c147c417f3_2c405c90e2bbd6df13bb289f52516642.png)
cette approximation est puissante, et peut même donner parfois un résultat exact, comme par exemple dans le cas où le potentiel est celui d'un oscillateur harmonique de fréquence ω. Dans ce cas, la fonction Ψ doit satisfaire, en plus des conditions de bord:
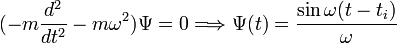
et on obtient l'expression exacte du propagateur de l'oscillateur harmonique, par l'approximation semi-classique:
![K_{ho}(x_{f},t_{f};x_{i},t_{i}) = \sqrt{\frac{m \omega}{2 \pi i \hbar \sin \omega(t_{f}-t_{i})}}\cdot e^{i S[x_{c}]/ \hbar}](https://static.techno-science.net/illustration/Definitions/autres/2/2ab2a18072011a587efc8f885ee46092_02c76a2c9aafabf900e1116cd66c036f.png)
avec l'action classique de l'oscillateur harmonique:
![S_{cl}[x]= \int_{t_{i}}^{t_{f}} dt \mathcal{L}[x,\dot{x}] = \frac{m\omega}{2}\left[(x_{f}^{2}+x_{i}^{2})\cot\omega (t_{f}-t_{i})-\frac{2x_{i}x_{f}}{\sin\omega (t_{f}-t_{i})}\right]](https://static.techno-science.net/illustration/Definitions/autres/0/08fa3dfef8fd286276232bc536be0a08_1e7b5c142149b7a91af68c2f6ea0b0a6.png)
à noter une autre formulation équivalente de l'approximation semi-classique, dite de Van Vleck-Pauli-Morette, qui découle directement de la précédente: