Limite de Roche - Définition

Introduction

La limite de Roche est la distance théorique en dessous de laquelle un satellite commencerait à se disloquer sous l'action des forces de marée causées par le corps céleste autour duquel il orbite, ces forces dépassant la cohésion interne du satellite. Elle tire son nom de l'astronome français Édouard Roche qui l'a théorisée le premier. La limite de Roche possède un analogue dans le domaine galactique : le rayon de marée.

Considérez un corps fluide qui maintient sa structure par sa gravité et qui orbite un objet massif, vu ici par le dessus du plan orbital. Éloigné de la limite de Roche, sa forme est sphérique.

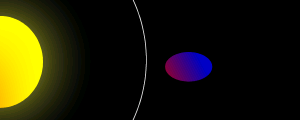
Plus près de la limite le corps est déformé par les forces de marée.

À l'intérieur de la limite la gravité du fluide n'est plus suffisante pour maintenir la structure du corps, et les forces de marée le désintègrent.

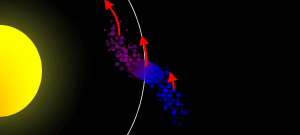
Les flèches rouges représentent le déplacement des restes du satellite. Les particules plus proches orbitent plus rapidement que celles plus éloignées.

La différence de vitesse orbitale finit par former un anneau à partir des particules du corps initial.

Estimation

Le calcul de la limite de Roche est par essence un problème complexe, car il dépend de la constitution interne du satellite. Cependant, des approximations peuvent être faites.

Historiquement, Roche avait considéré la distance à laquelle deux sphères indéformables de rayon r et de masse m, en contact, orbitant autour d'une planète de masse M et de rayon R, se détacheraient sous l'effet des forces de marées. Cette distance est égale à :

où ρ_P la masse volumique moyenne de la planète et ρ_s celle du satellite.

Il est également possible de calculer la distance à laquelle un petit morceau du satellite - de masse µ - maintenu par la force d'attraction gravitationnelle de celui-ci, commence à se détacher (c'est le cas dit « rigide ») :

Ces deux calculs ne tiennent cependant pas compte de la déformation du satellite sous l'effet des forces de marées. Si on considère que la cohésion du satellite est maintenue par les seules forces de gravitation internes (un satellite liquide, en quelque sorte), il se déforme en un ellipsoïde (c'est le cas dit « fluide »). Le problème demande la solution d'une équation transcendante qui ne peut se faire que numériquement. Roche travaillait dans la deuxième moitié du XIX^e siècle et n'avait pas les moyens de calcul que nous avons maintenant. Sa solution était :

La véritable solution est (voir pour les détails du calcul):

C'est cette dernière valeur qui est utilisée à l'heure actuelle.

Lobes de Roche

Dans un système stellaire binaire, un lobe de Roche est la région de l'espace où les particules sont gravitationnellement liés à l'une ou l'autre des étoiles. Ces deux régions, chacune formant une « larme » entourant l'une des étoiles, se rejoignent au point de Lagrange L₁ du système.

Si l'une des deux étoiles s'étend au-delà de son lobe de Roche, la matière concernée « tombe » vers l'autre étoile. Ce processus peut conduire à terme à la désintégration totale de l'étoile, chaque perte de matière réduisant d'autant le lobe.

Dans le cas d'un couple géante rouge / naine blanche, du gaz provenant de la géante peut dépasser son lobe de Roche et provoquer plusieurs novae.