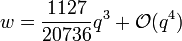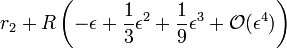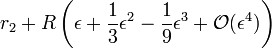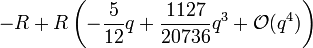Point de Lagrange - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un point de Lagrange (noté L à L), ou, plus rarement, point de libration, est une position de l'espace où les champs de gravité de deux corps en orbite l'un autour de l'autre, et de masses substantielles, se combinent pour compenser exactement la force centrifuge. Dans le cas où les deux corps sont en orbite circulaire, ces points représentent les endroits où un troisième corps de masse négligeable resterait immobile par rapport aux deux autres, au sens où il accompagnerait à la même vitesse angulaire leur rotation autour de leur centre de gravité commun sans que sa position par rapport à eux n'évolue. Au nombre de cinq, ces points se scindent en deux points stables dénommés L et L, et en trois points instables notés L à L. Ils sont nommés en l'honneur du mathématicien français Joseph-Louis Lagrange. Ils interviennent dans l'étude de certaines configurations d'objets du Système solaire (principalement pour les points stables) et dans le placement de divers satellites artificiels (principalement pour les points instables). Ce sont les points remarquables de la géométrie de Roche (points-col et extremums) laquelle permet notamment de classer les différents types d'étoiles binaires.
Historique
En mécanique céleste, il est un sujet qui a passionné de nombreux mathématiciens : c'est le problème dit des trois corps. Newton, après avoir énoncé sa loi qui exprime que « les corps s'attirent avec une force proportionnelle au produit de leur masse et inversement proportionnelle au carré de la distance de leurs centres », a cherché à décrire le comportement de trois corps sans y parvenir. Il faut attendre le mathématicien Joseph-Louis Lagrange qui, en 1772, étudia le cas d'un petit corps, de masse négligeable (ce qu'on appelle aujourd'hui corps d'épreuve ou particule-test), soumis à l'attraction de deux plus gros : le Soleil et, par exemple, une planète. Il découvrit qu'il existait des positions d'équilibre pour le petit corps, des endroits où toutes les forces se compensent.
Calcul de la position des points de Lagrange
Le calcul de la position des points de Lagrange se fait en considérant l'équilibre d'un corps de masse négligeable entre le potentiel gravitationnel créé par deux corps en orbite et la force centrifuge. La position des points L et L peut être obtenue analytiquement. Celle des trois autres points L à L s'obtient en résolvant numériquement ou éventuellement à l'aide d'un développement limité une équation algébrique. La position de ces trois points est donnée dans le tableau ci-dessous dans le cas où la masse d'un des deux corps (en l'occurrence le numéro 2) est négligeable devant l'autre, situé à une distance R du précédent. Les positions sont données le long de l'axe reliant les deux corps, dont l'origine est identifiée au centre de gravité du système, et dont l'orientation va du corps 1 au corps 2. Les quantités r et q dénotent respectivement la position du corps 2 sur l'axe et le rapport de la masse du corps le plus léger à la masse totale des deux corps. Enfin, on utilise la quantité ε définie par ε = (q / 3)1/3.
| Point | Position par rapport au centre de gravité du système |
|---|---|
| L |
|
| L |
|
| L |
|
Dans la littérature, on trouve parfois des expressions quelque peu différentes, du fait que l'origine de l'axe est prise ailleurs que sur le centre de gravité, et que l'on utilise comme terme à la base du développement limité le rapport entre les deux masses plutôt que le rapport de la plus petite à la masse totale, c'est-à-dire que l'on utilise parfois la quantité q' définie par
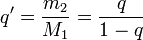
- Préliminaires
On note M et m la masse des deux corps, la masse du premier étant supposée supérieure ou égale à celle du second. Les deux corps sont supposés être en orbite circulaire, leur séparation étant R. Les deux corps orbitent autour de leur centre de gravité commun. On note r et r les distances algébriques des deux corps par rapport à un axe orienté du corps 1 au corps 2 (c'est-à-dire que r va être négatif et r positif). Le centre de gravité est défini par l'équation
- M1r1 + m2r2 = 0,
avec par définition, de la distance R,
- r2 − r1 = R.
Ces deux équations ont pour solution
-
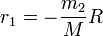
-
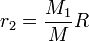
où on a noté M = M + m la masse totale du système.
Les deux corps orbitent l'un autour de l'autre à une vitesse angulaire ω, dont la valeur est donnée par la troisième loi de Kepler :
-
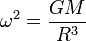
G étant la constante de gravitation.
Si l'on se place dans le référentiel tournant avec les deux corps, c'est-à-dire à la vitesse angulaire ω, un corps immobile sera soumis, outre aux forces gravitationnelles des deux corps, à la force centrifuge. Si on notre r le rayon vecteur de ce corps, la force centrifuge par unité de masse f à laquelle il sera soumis s'écrit
-
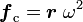
La définition d'un point de Lagrange est que la somme des forces gravitationnelles et inertielles s'annule en ces points. En notant r le rayon vecteur du ou des points en question, on a ainsi
-
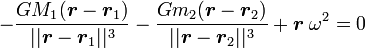
les doubles barres indiquant que l'on prend la norme des vecteurs considérés. On remplace ensuite la vitesse angulaire ω par sa valeur issue de la troisième loi de Kepler, ce qui donne
-
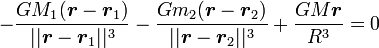
que l'on simplifie immédiatement par la constante de gravitation
-
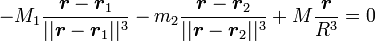
C'est la résolution de cette équation qui donne les différents points de Lagrange.
- Les deux cas à considérer
La projection de cette équation perpendiculairement au plan de l'orbite, dont la normale est donnée par un vecteur noté
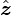
-
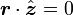
ce qui implique que l'ensemble des points de Lagrange est situé dans le plan de l'orbite. La résolution de l'équation se fait donc dans le plan orbital. Deux cas sont à considérer :
- celui où l'on cherche un point le long de l'axe formé par les deux corps,
- celui où l'on cherche un point en dehors de cet axe.
- Cas des points L et L
On suppose que le rayon vecteur r n'est pas parallèle à l'axe passant par les deux corps. On projette donc l'équation fondamentale perpendiculairement à cet axe, direction que l'on suppose définie par un vecteur noté
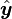
-
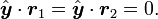
L'équation fondamentale se réécrit donc
-
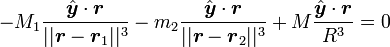
Les termes en
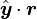
-
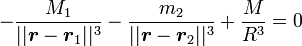
On définit maintenant la direction
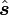
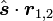
-
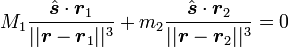
Or, d'après le théorème de Thalès, les projections de r et r le long de
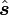
- .
Le barycentre des deux corps implique, comme vu précédemment, que
- M1r1 + m2r2 = 0.
La combinaison de cette équation et celle qui précède implique donc que les deux distances
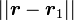
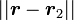
-
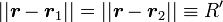
En injectant ce résultat sur la projection le long de r, il vient alors
-
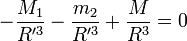
En multipliant le tout par R'3 et en se souvenant que M est la somme des deux masses, on obtient finalement
-
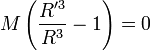
ce qui donne au final
-
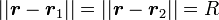
c'est-à-dire que les points cherchés forment un triangle équilatéral avec les deux corps du système. Ces triangles sont de plus inclus dans le plan orbital, ce qui donne deux points possibles, notés comme annoncé L et L, étant situé de part et d'autre de l'axe reliant les deux corps.
En utilisant le théorème de Pythagore, la distance D de ces deux points de Lagrange du centre de gravité du système s'écrit
-
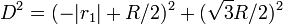
ce qui donne
-
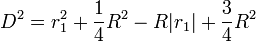
ce qui donne
-
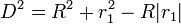
En utilisant le fait que R = | r1 | + r2, il vient
-
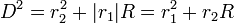
- Cas des points L à L
Dans le cas où l'on considère des points de Lagrange situés sur l'axe reliant les deux corps, trois sous-cas sont à considérer :
- Le cas où le ou les points sont entre les corps 1 et 2 ;
- Le cas où le ou les points sont à l'opposé du corps 2 par rapport au corps 1 ;
- Le cas où le ou les points sont à l'opposé du corps 1 par rapport au corps 2 .
Dans ces trois cas, l'équation fondamentale se réécrit de la façon suivante :
- Cas 1 : la projection des deux forces sur l'axe a des signes opposés (la projection de la force exercée par le corps 1 est négative, celle de la force exercée par le corps 2 est positive), ce qui donne
-
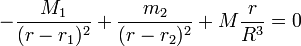
-
- avec
- r1 < r < r2.
- Cas 2 : la projection des deux forces sur l'axe est négative, ce qui donne
-
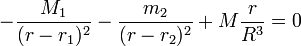
-
- avec
- r1 < r2 < r.
- Cas 3 : la projection des deux forces sur l'axe est positive, ce qui donne
-
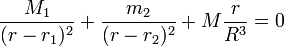
-
- avec
- r < r1 < r2.
Chacune de ces trois équations peut se ramener à une équation polynomiale du cinquième degré, pour laquelle il n'existe pas de solution analytique exacte, sauf cas particulier (comme celui des deux masses identiques par exemple).
L'unicité des solutions dans chacun des trois cas se déduit du fait que l'équation à résoudre sur l'équilibre des forces dérive d'un potentiel U, donné par
-
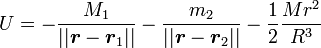
- Forme réduite et solution dans le cas où le rapport entre les masses est faible
Quand le rapport entre m et M (ou entre m et M) est faible, on peut trouver une solution approchée pour la position de chacun des points en effectuant un développement limité à partir d'une solution approchée facile à trouver. Pour simplifier les notations, on effectue un changement d'échelle afin d'exprimer toutes les longueurs en unité de la séparation R et les masse en unité de la masse totale M. On pose ainsi
- u = r / R,
et
- u1,2 = r1,2 / R,
et on définit le petit paramètre q par
-
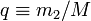
à partir de quoi on peut exprimer
- M1 / M = 1 − q,
- u1 = q,
- u2 = 1 − q.
Dans ce cas là, les trois équations écrites ci-dessus prennent la forme plus simple
- Cas 1 :
-
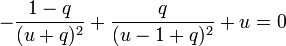
-
- avec
- − q < u < 1 − q.
- Cas 2 : la projection des deux forces sur l'axe est négative, ce qui donne
-
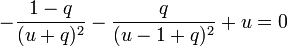
-
- avec
- 1 − q < u.
- Cas 3 : la projection des deux forces sur l'axe est positive, ce qui donne
-
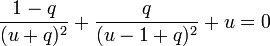
-
- avec
- u < − q.
- Le point L
Quand la masse du corps 2 est négligeable, l'attraction de celui-ci est négligeable sauf si la particule d'épreuve est très proche. Or, quand l'attraction du corps 2 est négligeable, l'équilibre entre l'attraction du corps 1 et la force centrifuge est tel que la distance du point d'équilibre est de l'ordre de R. Quand le point d'équilibre est situé à l'opposé du corps 2, on est dans le cas du point de Lagrange L, qui est donc, en gros, situé à l'opposé du corps 2 par rapport au corps 1. Dans le cas contraire, on va donc supposer que le point d'équilibre est plutôt proche du corps 2 (et donc à nouveau situé à la distance R du corps 1), mais néanmoins suffisamment éloigné pour que l'attraction du corps 2 exercée sur la particule d'épreuve reste petite par rapport à celle du corps 1. On pose donc à partir de la forme réduite
- u = u2 + ε' = 1 − q + ε,
où ici ε' est une quantité petite et négative (on suppose ici que le point est entre les deux corps). L'équation réduite se transforme alors en
-
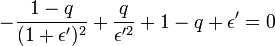
On effectue un développement limité au premier ordre de l'attraction produite par le corps 1 :
-
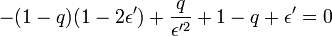
Les termes en 1 - q se simplifient, et il reste
-
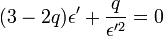
Toujours en ne gardant que les termes d'ordre le plus bas en q, il vient
-
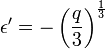
On peut par la suite continuer le calcul, en développement l'écart du point au corps 2 en puissances de ε'. On pose ainsi
-
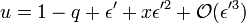
L'équation fondamentale réduite donne alors
-
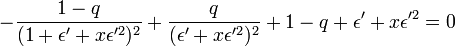
On peut factoriser le second terme avec q / ε'2, que l'on peut remplacer par sa valeur, soit -3 ε'. On obtient alors
- − (1 − q)(1 + ε' + xε'2) − 2 − 3ε'(1 + xε') − 2 + 1 − q + ε' + xε'2 = 0.
On effectue ensuite un développement limité des deux premiers termes, au second ordre pour le premier et au premier ordre pour le suivant, ce qui donne
- − (1 − q)(1 − 2ε' − 2xε'2 + 3ε'2) − 3ε'(1 − 2xε') + 1 − q + ε' + xε'2 = 0,
d'où on déduit que x vaut un tiers, ce qui donne
-
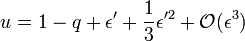
Le développement peut ensuite être continué suivant la même procédure. À l'ordre suivant, on a ainsi
-
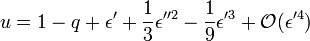
- Le point L
Le cas du point L se résout exactement comme dans la section précédente, si ce n'est que le signe du second terme de l'équation fondamentale est négatif. On pose donc
- u = 1 − q + ε,
ε étant cette fois-ci supposé petit et positif, et on a ainsi
-
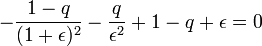
La résolution à l'ordre le plus bas donne
-
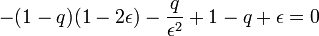
qui après annulation des termes donne
-
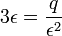
soit
-
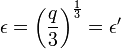
Cela correspond au signe près au même résultat que précédemment. La suite du développement de la solution se fait de même que précédemment. On part de
- u = 1 − q + ε + xε2,
et on injecte ce résultat dans l'équation fondamentale
-
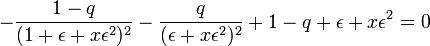
Comme précédemment, on transforme cette expression selon
- − (1 − q)(1 − 2ε − 2xε2 + 3ε2) − 3ε(1 − 2xε) + 1 − q + ε + xε2 = 0,
ce que l'on résout en
-
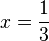
soit
-
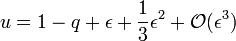
Cette expression est identique à celle du premier point de Lagrange en remplaçant ε' par ε, mais ces deux points sont dissymétriques : comme le signe de ε, ε' change entre le point L et le point L, la correction du second ordre, toujours positive, rapproche le point L du corps 2 alors qu'elle éloigne le point L : les deux points ne sont plus à égale distance du corps 2. Pour la Terre, le rapport de masse est de 1 / 300 000, et ε est de l'ordre 0,01, ce qui place les deux points par rapport à la Terre à une distance d'environ un centième de la distance Terre-Soleil, soit dans les 1 500 000 kilomètres. Le terme de second ordre est de l'ordre d'un trente-millième de la distance Terre-Soleil, soit dans les 5 000 km. Le point L est donc environ 10 000 km plus près de la Terre que ne l'est L.
Enfin, on peut poursuivre le développement à l'ordre supérieur, ce qui donne, tous calculs faits
-
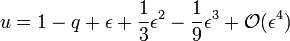
- Le point L
Dans le cas 3, qui va correspondre au point L, l'équation fondamentale s'écrit
-
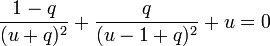
Comme le point est supposé au-delà du corps 1 par rapport au corps 2, il est plus proche du corps le plus massif, dont l'attraction va être prépondérante par rapport à l'autre corps. Dans la situation où l'on se place, le point recherché a donc sa position approximée par
-
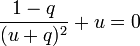
La solution approchée de cette équation est bien sûr
-
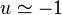
Pour trouver les écarts à cette valeur, on écrit dans l'équation fondamentale
- u = − 1 + v,
et on résout l'équation en prenant en compte les premiers termes en q. On obtient ainsi
-
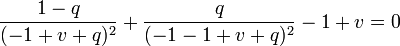
Les quantités v et q étant petites devant R, le premier terme s'écrit
-
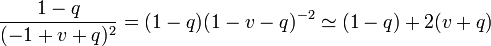
Le second terme étant négligeable par rapport au précédent (il est proportionnel à q), il peut s'approximer en
-
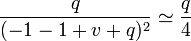
En combinant l'ensemble de ces termes, on obtient
-
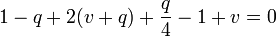
ce qui donne
-
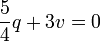
c'est-à-dire
-
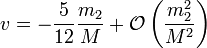
On peut sans difficulté continuer ce calcul en posant désormais
-
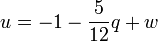
w étant cette fois proportionnel à q2. L'équation fondamentale devient alors
-
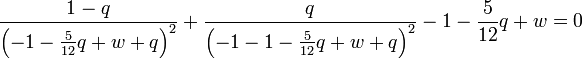
c'est-à-dire
-
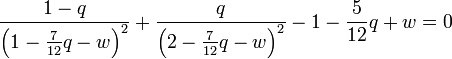
En développant cette expression au second ordre en q, on trouve
-
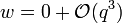
c'est-à-dire que w est au plus en q3. En refaisant le calcul dans ce cadre là, on trouve finalement
-