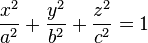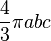Ellipsoïde - Définition
En mathématiques, un ellipsoïde est une surface du second degré de l'espace euclidien à trois dimensions. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de point à l'infini.

L'ellipsoïde admet un centre et au moins trois plans de symétrie. L'intersection d'un ellipsoïde avec un plan est une ellipse, un point ou l'ensemble vide.
Dans un repère bien choisi, son équation est de la forme
où a, b et c sont des paramètres strictement positifs donnés, égaux aux longueurs des demi-axes de l'objet.
Dans le cas très particulier où a = b = c, la surface est une sphère de rayon a.
Dans le cas où seuls deux paramètres sont égaux, l'ellipsoïde peut être engendrée par la rotation d'une ellipse autour d'un de ses axes. Il s'agit d'un ellipsoïde de révolution, qu'on retrouve sous forme de miroirs elliptiques dans les projecteurs de cinéma. On montre aussi que cette surface est optimale pour les dirigeables.
Volume
Le volume d'un ellipsoïde défini par l'équation ci-dessus vaut: