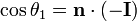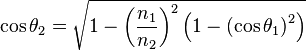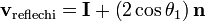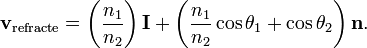Lois de Snell-Descartes - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Bibliographie
Pour l'histoire de l'optique :
- BLAY M. Les figures de l’arc-en-ciel. Paris : Belin, Coll. Pour la science, 2005.
- RONCHI V. Histoire de la lumière, (Reimpr.), Paris : Ed. Jacques Gabay, 1996.
Forme vectorielle des lois de Snell-Descartes
La forme vectorielle permet d'exprimer les vecteurs directeurs des rayons réfléchi et réfracté à partir du vecteur directeur du rayon incident. Le résultat est identique à celui des formes scalaires, mais sous forme de vecteurs au lieu d'angles.
Étant donné le vecteur directeur I du rayon incident (en provenance d'une source lumineuse et en direction du dioptre) et le vecteur normal n au plan incident, on a :
Note :
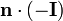
La réflexion totale a lieu quand le radicande de la formule de cosθ2 est négatif.