Lois de Snell-Descartes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les lois de Snell-Descartes décrivent le comportement de la lumière à l'interface de deux milieux. Ces lois sont au nombre de trois, une pour la réflexion et une pour la réfraction. Avec la propagation rectiligne de la lumière dans les milieux homogènes et isotropes, ces lois sont à la base de l'optique géométrique.
Historique
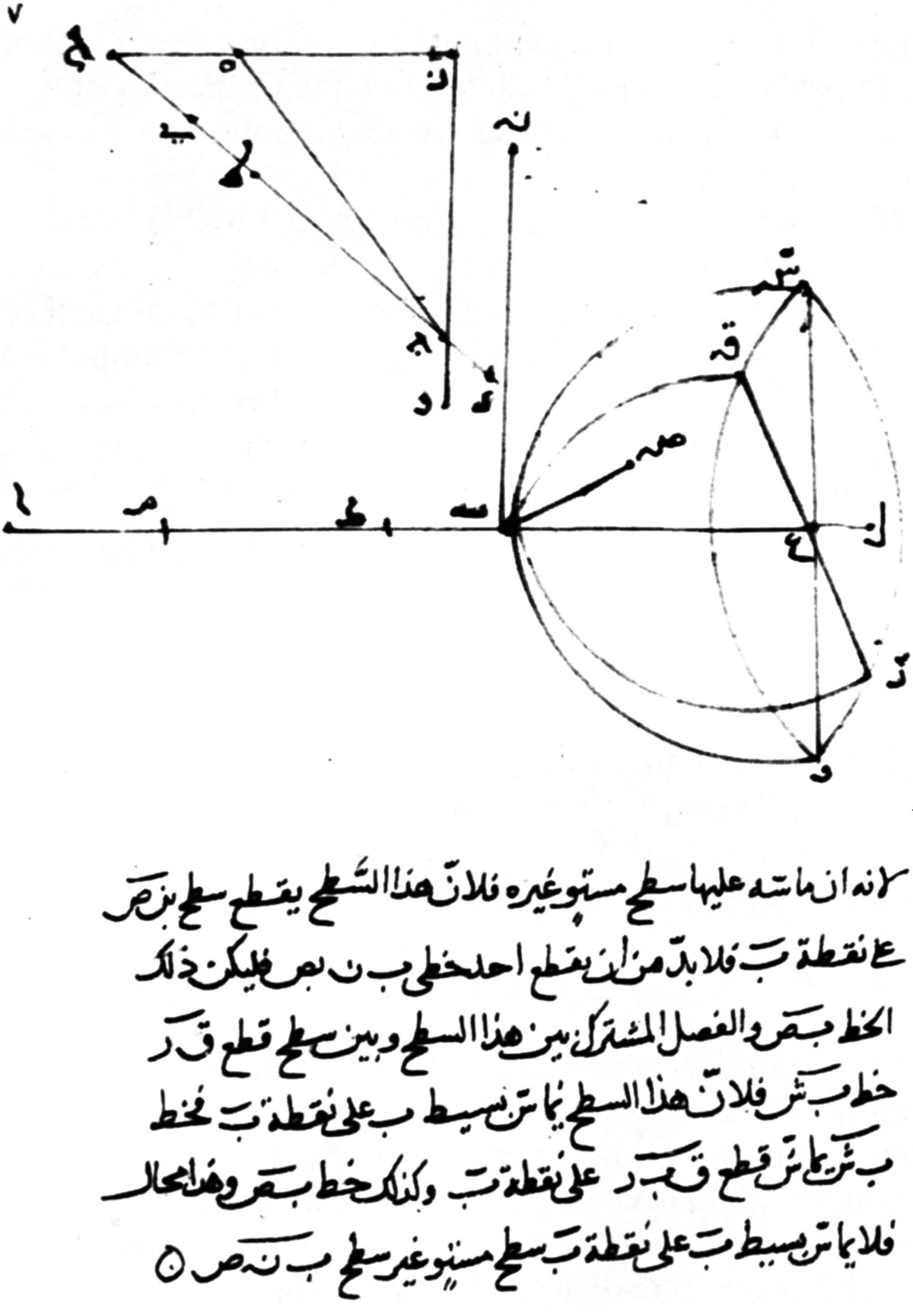
La loi de la réfraction est connue de Ibn Sahl (c. 940-1000), en 983. En particulier, il calcule la "lentille anaclastique parfaite". Plus tard, la théorie de l'arc-en-ciel est connue dans le monde arabe (Al Farisi).
Ensuite, en Europe, à la suite de la traduction latine du Traité d'optique (Alhacen), l'optique se répand : Oxford ( Robert Grossetête, Roger Bacon, Paris, Prague . La loi des petits angles est connue : Witelo (dit Vitellion) aurait repris les tables expérimentales de déviation établies par Ptolémée, mais c'est ensuite Kepler qui, dans les Paralipomènes à Vitellion, a énoncé explicitement la relation entre les (petits) angles d'incidence et de réfraction.Harriot est crédité d'avoir dressé des tables via la loi des sinus ( 1601) et d'expliquer l'arc-en-ciel(1606); mais il ne publie pas.
- Snell développe ses travaux, en même temps qu'il publie sa table des sinus (1621).
- Descartes publiera, en 1637, la loi dans son traité de Dioptrique (en annexe du Discours de la Méthode) .
- Les lois de Snell-Descartes peuvent être entièrement déduites du principe de Fermat, et en physique moderne des équations de Maxwell de l'électromagnétisme.
En Europe occidentale, la querelle de priorité- Snell ou Descartes ? - fût abondamment débattue ;compte-tenu de Ibn Sahl, Harriot, Kepler, c'est une "ancienne" querelle (voir controverses du cartésianisme, dioptrique ).
En Europe occidentale, l'énoncé de la loi des sinus est attribuée à la fois à Descartes et à Snell, et ce fait sera l'objet d'une querelle de priorité si fréquente à cette époque ( début du XVIIe) : la polémique portant sur la question de savoir si Descartes a lui-même découvert cette loi ou simplement eu connaissance de celle établie peu de temps auparavant par Snell, ce dernier étant décédé sans l’avoir publiée. Si Leibniz et Huygens considéraient qu’en effet Descartes ne pouvait pas avoir été sans connaître la loi énoncée par Snell, les avis des historiens ne sont pas si tranchés. B. Maitte évoque la connaissance que Descartes aurait eue du manuscrit de Snell non publié (qui, selon J.-P. Maury, aurait été confié à Rivet, professeur de théologie en relation avec le Père Mersenne, lui-même correspondant beaucoup avec Descartes). Mais selon P. Costabel il n’y a aucune preuve en l’état actuel de la documentation historique quant au fait que Descartes ait eu communication du résultat de Snell. D’autres auteurs évoquent l’antériorité de Harriot qui aurait trouvé ladite loi mais n’aurait fourni à Kepler que les tables des mesures sans l’interprétation.
Les documents historiques actuellement retrouvés ne permettent pas de connaître la démarche de Snell. Pour ce qui concerne Descartes, quelques indications conduisent à considérer que l’idée des sinus fut directement liée à la recherche de la forme d’une lentille dite "parfaite", c’est-à-dire capable de faire converger exactement en un point un faisceau de rayons parallèles. Le profil pressenti du dioptre était celui d’une hyperbole et c’est l’étude géométrique de ce profil – qualifié d’anaclastique – qui a conforté Descartes dans le bien-fondé d’une loi en sinus : la conviction, pour ne pas dire la preuve, a résulté d’un ensemble de considérations, expérimentales (fabrication à la limite du possible d’une telle lentille par Ferrier) et théoriques (démonstration que la forme hyperbolique correspondait bien à une relation entre les sinus des angles par le géomètre Mydorge et par le mathématicien Beeckman). Ajoutons ici que cette préoccupation est née de l’invention de la lunette, lunette améliorée par Galilée et transmise à Kepler qui en a donné une première explication.

















































