Matériau composite - Définition

Bibliographie

• Matériaux - Tome 2. Microstructure et mise en oeuvre - chapitre 25 - auteurs : Ashby et Jones - Dunod (1991)
• Traité des Matériaux - Presses Polytechniques et Universitaires Romandes - Site des PPUR

Vol. 1 : Introduction à la Science des Matériaux - 3è édition - chapitre 16 - ISBN 2-88074-402-4

Vol. 15 : Matériaux Composites à Matrices Organiques - ISBN 2-88074-528-4

• Des Matériaux - chapitre 14 - auteurs : Dorlot, Baïlon, Masounave - Éditions de l'École Polytechnique de Montréal (1986)
• Matériaux réfractaires et céramiques techniques - chapitre 25 - auteur : G. Aliprandi - Editions Septima (1989)
• Technologie des composites - auteur : Maurice Reyne - Hermes (1995) - ISBN 2-86601-455-3 harry potter

Description mécanique

Formalisation

Le comportement d'un matériau composite se décrit de la façon suivante, en utilisant le formalisme de la mécanique des milieux continus :

• on a n matériaux différents qui forment le composite (on parle de « phases », caractérisées par leur fraction volumique et leur géométrie)
• A l'intérieur de chaque phase, le matériau peut se déformer et subir des contraintes. La déformation se fait selon la loi de comportement du matériau en question (que l'on connaît) : pour le cas linéraire.
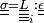
• Il y a équilibre des forces volumiques, soit, dans chaque matériau i : si l'on néglige la force de pesanteur devant les forces appliquées au matériau (pression, traction, cisaillement).
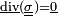
• Enfin, l'agrégation des comportements de chaque matériau simple, pour aboutir au comportement du composite, nécessite de décrire l'équilibre des forces entre deux matériaux « collés », en chaque point de leur surface de contact. Cette condition est que la force exercée par le matériau 1 sur le matériau 2 à la surface de contact ( si désigne le vecteur unitaire perpendiculaire à la surface) doit être opposée à celle exercée par le matériau 2 sur le matériau 1. Ceci implique une certaine continuité du champ de contraintes  : on doit avoir (en chaque point des surfaces de contacts des matériaux mélangés dans le composite) . C'est par cette condition qu'intervient la microgéométrie du mélange dans la détermination du comportement du composite. Ainsi, en mélangeant des matériaux isotropes selon une géométrie non isotrope (fibres, feuilles...), on obtient un composite non isotrope mais dont les propriétés mécaniques sont issues des celles des matériaux initiaux !
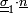
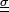
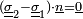
• Ainsi, le matériau composite est décrit en chacun de ces points. La loi de comportement du composite qui en résulte doit pouvoir faire le lien entre les déformations macroscopiques et les contraintes macroscopiques (c'est-à-dire leurs valeurs moyennes, car par exemple si l'on mélange un matériau mou et un dur, les déformations microscopiques seront très variables selon le matériau, et c'est la déformation globale que l'on observera à l'échelle du composite). Cette loi de comportement du composite est dite « effective » : on note dans le cas linéaire.

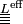
Résolution

Le problème précédent ne se résout pas simplement, sauf dans le cas de géométries très simples (inclusions sphériques, fibres, feuilles empilées, ou de manière générale dans le cas d'inlusions de forme ellipsoïdale).

Des recherches visent à décrire le comportement du composite sans forcément en connaître la géométrie exacte, en essayant de borner l'énergie de déformation du composite (l'énergie de déformation d'un matériau est ). On peut ainsi citer les bornes de :

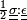
• Voigt et Reuss :
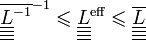
  Les cas extrêmes de ces inégalités sont atteignables par des géométries de couches empilées. D'ailleurs, on retrouve ici un résultat constant de la physique : la résistance électrique d'un assemblage de résistances est la somme des résistances lorsqu'elles sont en série, ou est l'inverse de la somme des inverses quand elles sont en parallèle (résultat similaire également avec un assemblage de ressorts). La différence est qu'ici la loi de comportement n'est pas décrit par un scalaire (comme c'est le cas pour une résistance électrique ou une raideur de ressort), mais par une grandeur multidimensionnelle (le tenseur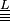 d'ordre 4).
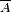
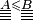
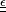
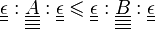
  NB : ici désigne la moyenne de sur tout le volume du composite ; et l'inégalité entre tenseurs s'entend au sens où pour tout tenseur on a

• Hashin et Shtrikman : bornes plus précises, dans le cas isotrope.

La mécanique des composites est encore un domaine de recherche théorique active : comportement mécanique ou électrique, linéaire, non linéaire, viscoélastique, avec fissures ou plasticité, flambage...

Une limite de cette modélisation est que l'on ne peut pas connaître de manière précise la microgéométrie d'un composite réel : il y a toujours des défauts ; mais la modélisation permet de décrire de manière assez précise la loi de comportement.

Un autre intérêt de cette recherche théorique entre la géométrie d'un composite et sa loi de comportement est le mode de réalisation d'un matériau dont les caractéristiques mécaniques ont été obtenues par une optimisation informatique.