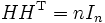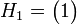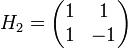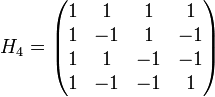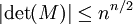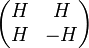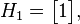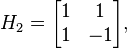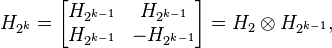Matrice de Hadamard - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une matrice de Hadamard est une matrice carrée dont les coefficients sont tous 1 ou -1 et dont les lignes sont toutes orthogonales entre elles. Le nom retenu pour ces matrices rend hommage au mathématicien français Jacques Hadamard, même si les premiers exemples systématiques sont dus à James Joseph Sylvester.
Pour une matrice H d'ordre n, la propriété d'orthogonalité des colonnes peut également s'écrire sous la forme
où In est la matrice identité d'ordre n.
Exemples :
Propriétés
Une matrice réelle M d'ordre n, dont les éléments sont bornés,
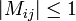
si et seulement si c'est une matrice de Hadamard.
Certaines opérations élémentaires transforment une matrice de Hadamard en une autre : permutation de lignes ou de colonnes, multiplication d'une ligne ou d'une colonne par -1.
La transposée d'une matrice de Hadamard est encore une matrice de Hadamard.
Construction de Sylvester
Les premiers exemples de matrices de Hadamard sont dus au mathématicien James Joseph Sylvester.
La construction est basée sur la propriété suivante. Si H une matrice de Hadamard d'ordre n, alors la matrice
est une matrice de Hadamard d'ordre 2n.
En appliquant cette construction de façon récursive, on construit la suite des matrices de Walsh, ou de Sylvester
puis (en utilisant la notation du produit de Kronecker)
Les matrices construites par la méthode de Sylvester ont certaines propriétés intéressantes. Ce sont des matrices symétriques de trace nulle. Les éléments de la première colonne et de la première ligne sont tous positifs. Dans chaque autre ligne ou colonne, la moitié des éléments est positive. Ces matrices sont étroitement liées aux fonctions de Walsh.
Application
Les matrices de Hadamard sont utilisées dans les codes correcteurs comme celui de Reed-Muller, ou encore pour réaliser les plans d'analyse sensorielle et les plans d'expériences factoriels.
Ordre d'une matrice de Hadamard
L'ordre d'une matrice de Hadamard est nécessairement 1, 2 ou un multiple de 4.
La construction de Sylvester montre qu'il existe des matrices de Hadamard d'ordre 2k pour tout entier naturel k.
Les matrices de Hadamard d'ordres 12 et 20 ont été construite par Hadamard. Raymond Paley démontra plus tard comment construire une matrice de Hadamard d'ordre q+1 lorsque q est une puissance d'un nombre premier congrue à 3 modulo 4. Il a également construit des matrices d'ordre 2*(q+1) avec q, puissance d'un nombre premier congrue à 1 modulo 4. Sa méthode utilise les corps finis. D'autres méthodes pour la construction de matrices de Hadamard sont maintenant connues.
Conjecture de Hadamard
La question ouverte la plus importante à propos des matrices de Hadamard est celle de leur existence. D'après la conjecture de Hadamard,
- une matrice de Hadamard d'ordre 4k existe pour tout entier positif k.
À la suite de l'annonce de la découverte d'une matrice de Hadamard d'ordre 428 le 21 juin 2004 par Hadi Kharaghani et Behruz Tayfeh-Rezaie, le plus petit ordre multiple de 4 pour lequel aucune matrice de Hadamard n'est connue est actuellement 668.
La conjecture de Hadamard devrait plutôt être attribuée à Paley.