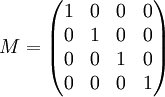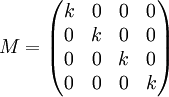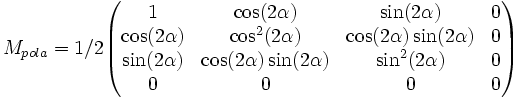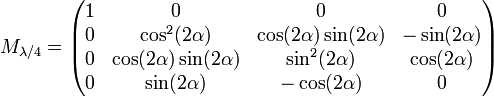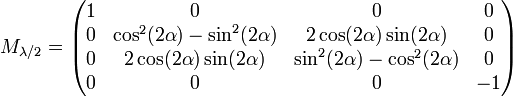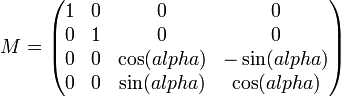Matrice de Mueller - Définition

Introduction

La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs qui représentent la polarisation de la lumière incohérente.

Description

Pour chaque composant optique, on trouve une matrice de Mueller.

Région isotrope, non absorbante

• Région vide, ou isotrope et non absorbante :

Région isotrope, absorbante

• Région isotrope avec un coefficient d'absorption 1-k (0<k<1) :

Polariseur linéaire

• Polariseur linéaire avec un angle de transmission α :

Lame de retard

• Lame de retard quart-d'onde avec azimut α pour l'axe rapide :

• Lame de retard demi-onde avec azimut α pour l'axe rapide :

• Lame de retard δ avec azimut α pour l'axe rapide :

Déphaseur