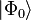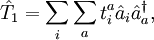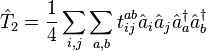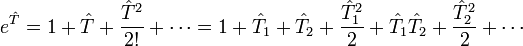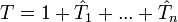Méthode du cluster couplé - Définition

L'opérateur cluster

L'opérateur cluster est écrit sous la forme :

,

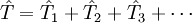
où est l'opérateur de toutes les excitations singulières, est l'opérateur de toutes les excitations doubles et ainsi de suite. Dans la formalisme de la seconde quantification ces opérateurs d'excitation sont exprimés de manière adéquate comme :

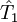
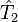
et ainsi de suite.

Dans la formule ci-dessus, et indiquent les opérateurs de création et de disparition respectivement, i, j sont utilisés pour les orbitales occupées et a, b pour les inoccupées. Les opérateurs de création et de disparition dans les termes de clusters couplés ci-dessous sont écrits dans une forme canonique, dans laquelle chaque terme est en ordre normal. Comme opérateurs d'excitation à une particule et à deux particules, et transforment la fonction de référence en une combinaison linéaire des déterminants de Slater simplement et doublement excités, respectivement. La résolution des coefficients inconnus et est nécessaire pour trouver la solution approchée .
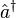
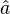
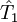
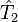
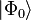
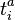
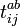
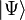
Si l'on prend en compte la structure de , l'opérateur exponentiel peut être développé en série de Taylor :

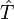
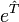
Cette série est finie en pratique car le nombre d'orbitales moléculaires occupées est fini, comme d'ailleurs le nombre d'excitations. Afin de simplifier la recherche des coefficients t, le développement de en opérateurs d'excitation individuels est achevé au deuxième ou à un niveau peu élevé d'excitation (rarement au-delà de quatre). Cette approche est garantie par le fait que même si le système admet plus de quatre excitations, la contribution de , , etc. à l'opérateur est faible. De plus, si le plus haut niveau d'excitation dans les opérateurs est n,

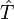
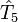
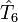
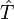
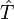
alors les déterminants de Slater excités plus de n fois peuvent (et habituellement le font) contribuent encore à la fonction d'onde en raison de la nature non-linéaire de l'ansatz exponentiel. Ainsi, le cluster couplé terminé à recouvre habituellement plus d'énergie de corrélation que l'interaction de configuration avec n excitations maximales.

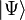
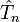
Description générale de la théorie

La complexité des équations et des codes de calcul correspondants, ainsi que le coût de calcul augmentent rapidement avec le niveau le plus élevé d'excitation. Pour de nombreuses applications, une précision suffisante peut être obtenue par CCSD, et la CCSD(T) plus précise (et plus coûteuse) est parfois appelée « l'étalon-or de la chimie quantique » pour son excellent compromis entre la précision et le coût pour des molécules proches des géométries d'équilibre. Des méthodes plus complexes comme la CCSDT et la CCSDTQ sont utilisées seulement pour des calculs de haute précision sur de petites molécules. L'inclusion de tous les n niveaux d'excitation pour un système à n électrons donne la solution exacte de l'équation de Schrödinger dans la base donnée.
Une amélioration possible pour une approche de cluster couplé standard est l'addition de termes linéaires dans les distances inter-électroniques par des méthodes comme CCSD-R12. Cela améliore le traitement de la corrélation électronique dynamique en satisfaisant la condition de col de Kato et accélère la convergence avec la base d'orbitales. Malheureusement, les méthodes R12 nécessitent la résolution de l'identité qui nécessite une base relativement importante afin d'être valides.
La méthode de cluster couplé décrite ci-dessus est connue comme la méthode de cluster couplé mono-référence (en anglais single-reference (SR) coupled-cluster method car l'ansatz exponentiel n'utilise qu'une fonction de référence . Les généralisations standard de la méthode SR-CC sont les approches multi-références (MR) : la méthode de cluster couplé d'état universel (state-universal coupled cluster en anglais, connu aussi comme la méthode cluster couplé dans un espace de Hilbert - Hilbert space coupled cluster), la méthode de cluster couplé de valence universelle (en anglais valence-universal coupled cluster, ou méthode de cluster couplé dans un espace de Fock - Fock space coupled cluster) et la méthode de cluster couplé sélective d'état (en anglais state-selective coupled cluster, ou encore méthode de cluster couplé d'état spécifique - state-specific coupled cluster).