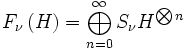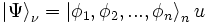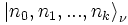Espace de Fock - Définition

L’espace de Fock est un espace de Hilbert utilisé en physique quantique pour décrire les états quantiques avec un nombre variable ou inconnu de particules.

L’espace de Fock se définit comme l’espace de Hilbert obtenu par la somme directe des produits tensoriels des espaces de Hilbert pour une particule.

où :

• est l'espace de Flock.
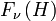
• S_ν est l’opérateur qui symétrise ou antisymétrise l’espace selon que l’espace de Fock décrit des particules obéissant aux statistiques de Bose-Einstein (bosons, ν = + ) ou de Fermi-Dirac (fermions, ν = − ).
• H est l’espace de Hilbert pour une particule. Il décrit les états quantiques pour une seule particule et pour décrire les états quantiques de systèmes avec n particules, ou des superpositions de tels états, il faut utiliser un espace de Hilbert plus large, l’espace de Fock, qui contient des états avec un nombre non limité et variable de particules. Les états de Fock sont la base naturelle de cet espace. (voir aussi Déterminant de Slater)

Exemple

Un exemple d’état de l’espace de Fock est

qui décrit n particules, une avec la fonction d'onde φ₁, la deuxième avec φ₂ et ainsi de suite et où φ_i est une fonction d’onde quelconque de l’espace de Hilbert H à une particule. Quand nous parlons d'une particule dans l’état φ_i, il faut garder à l’esprit qu’en mécanique quantique les particules identiques sont indiscernables et, dans un même espace de Fock, toutes les particules sont identiques (pour décrire plusieurs types de particules, il faut effectuer le produit tensoriel de plusieurs espaces de Fock différents). Une des propriétés les plus puissantes de ce formalisme est que les états sont intrinsèquement symétrisés correctement. Par exemple, si l’état ci-dessus est fermionique, il sera nul si deux (ou plus) des φ_i sont égaux car selon le principe d’exclusion de Pauli deux fermions (ou plus) ne peuvent pas être dans le même état quantique. De même, les états sont correctement normalisés, par construction.

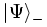
Une base utile et pratique pour cet espace est la base du nombre de particules. Si est une base de H, alors nous pouvons noter l’état avec n₀ particules dans l’état , n₁ particules dans l’état ,..., n_k particules dans l’état comme

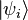
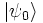
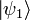
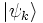
avec, bien sûr, si ν = − , chaque n_i prenant seulement les valeurs 0 ou 1 (autrement l’état est nul).

Un tel état est appelé un état de Fock. Puisque les sont des états stationnaires des champs libres, c’est-à-dire avec un nombre définis de particules, un état de Fock décrit une assemblée de particules sans interaction en nombre définis. L’état pur le plus général est une superposition linéaire des états de Fock.

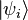
Deux opérateurs d’une immense importance sont les opérateurs de création et d’annihilation qui agissent sur un état de Fock en, respectivement, ajoutant et retirant une particule à l’état quantique décrit. Ils sont notés et respectivement, où φ est l’état quantique dans lequel la particule est ajoutée ou enlevée. Il est souvent utile de travailler avec des états de la base de H, ainsi ces opérateurs ajoutent et enlèvent exactement une particule dans l’état donné. Ces opérateurs servent aussi de base pour des opérateurs plus généraux agissant sur l’espace de Fock (par exemple, l’opérateur de nombre de particules dans l’état est ).

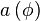
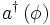
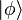
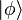
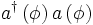
En pratique, on dispose générale des opérateurs de création et d’annihilation et l’on cherche à construire l’espace de Fock. On définit l’état du vide comme l’état qui est annulé par tous les opérateurs d’annihilation

pour tout φ

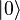
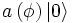
On peut ensuite construire les états à une particule en faisant agir l’opérateur de création sur l’état du vide : . On écrit aussi de manière abrégée . On procède de même pour les états à deux, trois... particules.

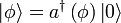
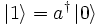
Ensuite, en utilisant la procédure mathématique standard de superposition linéaire et la complétion de Cauchy, on construit l’espace complet. L’espace résultant est l’espace de Fock recherché.