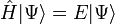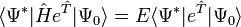Méthode du cluster couplé - Définition

Introduction

La méthode du cluster couplé, ou théorie du cluster couplé (expression souvent abrégée en « cluster couplé », en anglais coupled cluster) est une technique numérique de description des systèmes à plusieurs corps. Son utilisation la plus répandue est comme méthode ab initio de chimie quantique post-Hartree-Fock en chimie numérique. Il est basé sur la méthode d'orbitale moléculaire Hartree-Fock et lui ajoute un terme de correction afin de prendre en compte la corrélation électronique. Certains des calculs les plus précis pour des molécules de petite ou de taille moyenne utilisent cette méthode.
La méthode fut développée initialement par Fritz Coester et Hermann Kümmel dans les années 1950 afin d'étudier les phénomènes de physique nucléaire, mais devint plus fréquemment utilisée après que Jiři Čížek et Josef Paldus eurent reformulé la méthode pour l'adapter à la corrélation électronique dans les atomes et molécules dans les années 1960. Elle constitue à ce jour une des méthodes les plus répandues en chimie quantique incluant la corrélation électronique.

Ansatz de fonction d'onde

La théorie de cluster couplé donne une solution approchée à l'équation de Schrödinger indépendante du temps

où est le hamiltonien du système. La fonction d'onde et l'énergie de l'état de plus basse énergie sont notés respectivement et E. D'autres versions de la théorie de cluster couplé, comme la méthode de cluster couplé de l'équation de mouvement ou la méthode de cluster couplé multi-références peuvent aussi donner des solutions approchées des états excités du système.
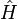
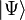
La fonction d'onde de la théorie du cluster couplé est écrite comme un ansatz exponentiel :

,

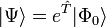
où est un déterminant de Slater construit habituellement à partir des orbitales moléculaires Hartree-Fock. est un opérateur d'excitation qui, lorsqu'il agit sur , produit une combinaison linéaire des déterminants de Slater (voir ci-dessous pour de plus amples détails).
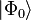
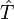
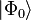
Le choix de l'ansatz exponentiel est opportun car (contrairement à d'autres, par exemple, l'interaction de configuration) il garantit l'extensivité de taille de la solution. La consistance de taille, dans la méthode de cluster couplé, dépend de la consistance de taille de la fonction d'onde référence.

Équations de cluster couplé

Les équations de cluster couplé sont des équations dont la solution est un ensemble de coefficients t. Il existe plusieurs façons d'écrire de telles équations mais le formalisme standard conduit à un ensemble final d'équations pouvant être résolu de manière itérative. L'approche variationnelle simple ne tire pas avantage de la nature connectée des amplitudes de clusters et conduit à un ensemble d'équations non achevé.
Supposons qu'il y ait q coefficients t afin de procéder à cette résolution : on a alors besoin de q équations. Il est aisé de noter que chaque coefficient t peut être mis en correspondance avec un certain détermant d'excitation : , qui correspond au déterminant obtenu à partir de par substitution des orbitales occupées i,j,k,... par les orbitales virtuelles a,b,c,.... En projetant l'équation de Schrödinger avec l'ansatz exponentiel par q différents déterminants par la gauche, on obtient les q équations recherchées :

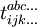
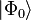
où par on entend l'ensemble complet des déterminants excités appropriés.

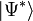
Malheureusement, est une série inachevée. Les équations de cluster couplé sont réduites à une forme proche dans la représentation de similarité transformée :

,

,

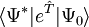
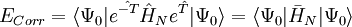
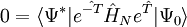
les dernières étant les équations à résoudre et les précédentes l'équation d'évaluation de l'énergie. Considérant la méthode standard CCSD :

,

,

,

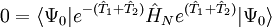
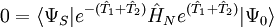
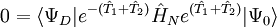
qui lorsqu'elle est factorisée en utilisant la formule de Baker-Campbell-Hausdorff pour le hamiltonien transformé de similarité , devient de degré 4 pour T₁ et quadratique pour T₂. Des codes standard de chimie quantique comme ACES ou NWChem résolvent les équations couplées en utilisant Ax = 0, où A est le jacobien du cluster couplé et x est le vecteur des amplitudes. En général, le hamiltonien transformé de similarité peut ne pas être hermitien.