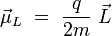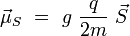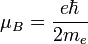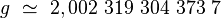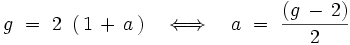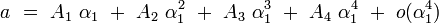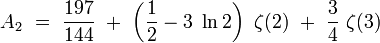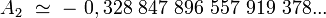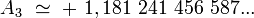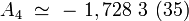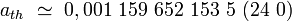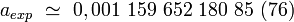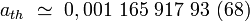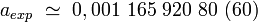Moment magnétique anomal - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique des particules, le moment magnétique anomal (et non « anormal ») désigne l'écart entre la valeur du facteur de Landé g d'un lepton et la valeur gDirac = 2 donnée par l'équation de Dirac. Cette anomalie est remarquablement bien expliquée par le modèle standard, en particulier par l'électrodynamique quantique, lorsque l'influence du vide quantique est prise en compte.
Rappels sur le moment magnétique de spin
Définition. Facteur de Landé
Au moment cinétique orbital d'une particule de charge q et de masse m est associé un moment magnétique orbital :
|
|
Le facteur q / 2m est appelé rapport gyromagnétique. De même, on associe à une particule de charge q, de masse m, et de spin donné un moment magnétique de spin :
|
|
où g est un nombre pur, appelé facteur de Landé (1921). Ce nombre varie selon la nature de la particule : on a approximativement g = 2 pour l'électron, g = 5.586 pour le proton, et g = − 3.826 pour le neutron.
Magnéton de Bohr
Pour l'électron, les valeurs propres du spin selon un axe sont
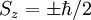
|
|
Moment magnétique anomal de l'électron
L'équation de Dirac prédit pour l'électron un facteur de Landé exactement égal à : g = 2. Or, la valeur expérimentale admise en 2005 vaut :
|
|
Il existe donc un écart, décelé pour la première fois en 1947 dans la structure hyperfine de l'hydrogène et du deutérium.
Anomalie
On est ainsi amené à introduire une anomalie a, définie par :
|
|
La théorie quantique des champs du modèle standard permet de calculer cette anomalie. La contribution dominante vient de l'électrodynamique quantique perturbative, et se présente sous la forme d'un développement en série de puissances de la constante de structure fine α, également appelée constante de couplage. Plus précisément, on est amené a écrire le développement suivant :
|
|
en puissances de
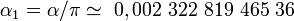
Note:
Le moment magnétique de l'électron est, à quelques millièmes près, égal au moment magnétique orbital, le magnéton de Bohr. Et cela se voit dès la première correction de Schwinger. En fait la valeur de la constante de structure fine est tirée de cette formule de QED (Quantum ElectroDynamique) et on obtient :
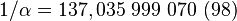
[à comparer avec la valeur CODATA : 137,035 999 11(46)? La "meilleure" valeur est sans doute 137,035 999 084 (51) selon la référence citée plus bas (fev 2008)]
Première correction de Schwinger
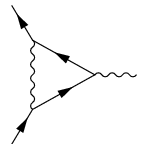
Le premier terme du développement, calculé par Schwinger en 1948, vaut simplement : A1 = 1 / 2. Ce fut le premier grand succès de la toute nouvelle électrodynamique quantique. Ce calcul, qui repose sur le diagramme de Feynman ci-contre, est aujourd'hui un exercice standard pour tout étudiant de troisième cycle débutant en théorie quantique des champs.
Malheureusement, les calculs des termes suivants sont beaucoup plus compliqués, car le nombre de diagrammes croit exponentiellement vite avec l'ordre du développement.
Correction d'ordre deux
Ce calcul fait intervenir 7 diagrammes de Feynman. Un premier résultat – erroné – a été publié en 1950, puis revu et corrigé en 1957-1958. On obtient :
|
|
dont la valeur numérique est :
|
|
où ζ(s) est la fonction zêta de Riemann, définie par :
 |
et vérifiant en particulier : ζ(2) = π2 / 6.
Correction d'ordre trois
Ce calcul fait intervenir 72 diagrammes de Feynman. Le calcul, commencé en 1969, n'a été terminé et publié qu'en 1996 (Laporta et Remmidi). On obtient une expression analytique assez compliquée (voir par exemple ) :
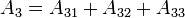
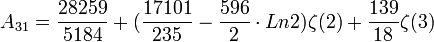
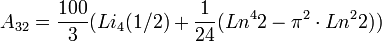
![A_{33} = [- 239\zeta(4) + 166\zeta(2)\cdot \zeta(3) -215\zeta(5)]/24](https://static.techno-science.net/illustration/Definitions/autres/0/0d67cffb399120647c8c47ec5a38252a_6c33e4b23db1cdae38016f3dec26ed83.png)
où
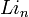
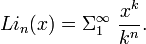
Numériquement, on obient :
|
|
Correction d'ordre quatre
Ce calcul, qui fait intervenir 891 diagrammes de Feynman, est impossible à faire entièrement à la main en un temps raisonnable ! Il a requis l'usage intensif de l'ordinateur. T.Kinoshita, a publié en 2006 le meilleur résultat numérique
|
|
- La correction d'ordre 5 n'a pas été évaluée mais on a seulement un intervalle de confiance.
On en tire l'anomalie dite universelle pour les leptons.
Comparaison théorie - expérience
Il convient alors de différencier les trois leptons e, µ, τ.
- pour l'électron : l'électron étant le lepton le plus léger, les contributions à son moment magnétique des autres leptons, des bosons vecteurs de l'interaction faible, et des quarks et gluons, sont petites, mais non négligeables à la précision actuelle. Leurs inclusions donne la prédiction théorique du modèle standard :
|
|
L'accord avec le résultats expérimental (2006,Odum, Phys.Rev.Lett 97) est à ce jour excellent :
|
|
- pour le muon : l'expérience n'est pas aussi satisfaisante. Il est vrai que le rapport de masse de ce pseudo-électron lourd est :
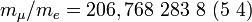
et les corrections sont plus importantes, en gros de 206².
La valeur de l'anomalie du muon est pourtant affinée par les récents résultats du BNL (Brookhaven Nat Lab). Mais les corrections théoriques sont plus élevées ; il faut outre les corrections entre leptons, prendre en compte les corrections de l'électro-faible, et celle des hadrons. A ce jour (2006) l'anomalie est :
|
|
|
|
soit environ 3 écarts-type de différence ce qui pose problème à l'heure actuelle (2008).
- pour le lepton tauon τ : sa masse est encore plus grande (1.77699 (29) GeV) et surtout sa durée de vie est 0.1 ps. Il est plus difficile à produire et la détermination de son anomalie n'a pas encore été réalisée.
Ceci dit, il restera toujours à évaluer la variation de α(E), qui jouera encore plus à ces énergies.