Moment cinétique orbital - Définition
Introduction
Le moment cinétique orbital est un concept de la mécanique quantique. C'est un cas particulier de moment cinétique quantique.
Analogies avec la mécanique classique
Le moment cinétique orbital correspond à la rotation d'une particule autour d'un noyau, comme la rotation d'un électron autour d'un noyau dans un atome.
On différencie le moment cinétique orbital du moment cinétique intrinsèque, interprétable par la rotation d'une particule élémentaire sur elle-même (on parle de spin de l'électron, par exemple).
Tout moment cinétique est quantifié en mécanique quantique (voir l'article moment cinétique quantique), c’est-à-dire que le moment cinétique ne peut prendre que des valeurs discrètes bien précises. C'est une des propriétés fondamentales de la théorie quantique.
Formules et formalisme quantique
L'opérateur de moment cinétique orbital est noté
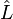
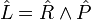
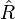
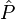
En représentation position, les composantes cartésiennes de l'opérateur
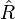
D'après ces définition, les composantes cartésiennes de l'opérateur de moment cinétique orbital s'écrivent :
On peut alors calculer les commutateurs de
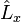
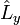
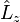
Moment cinétique total
L'opérateur de moment cinétique total noté
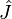
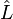
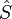
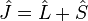
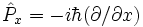
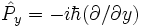
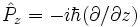
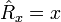
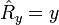
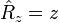
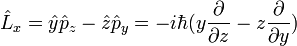
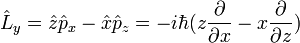
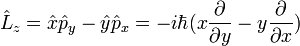
![[\hat L_x, \hat L_y] = i \hbar \hat L_z](https://static.techno-science.net/illustration/Definitions/autres/8/861c4c3f132e0f442680cf15210fd94a_c27144be9e0906c9d4d128170c7869c3.png)
![[\hat L_y, \hat L_z] = i \hbar \hat L_x](https://static.techno-science.net/illustration/Definitions/autres/0/023d8de4c789ba138219ab27574e1aa7_05a7ca5bc68c6a712633e05988248785.png)
![[\hat L_z, \hat L_x] = i \hbar \hat L_y](https://static.techno-science.net/illustration/Definitions/autres/7/7ab2f6cbdbc904a4ed89d3dab39061e2_a14d30993416cfdbb2291fb173673783.png)

















































