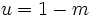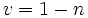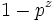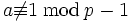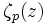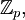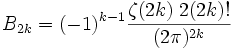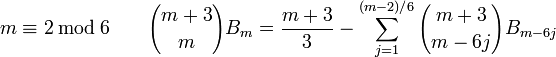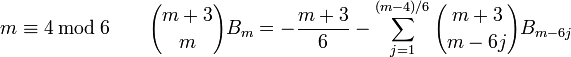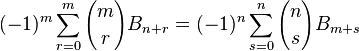Nombre de Bernoulli - Définition
La liste des auteurs de cet article est disponible ici.
Valeurs
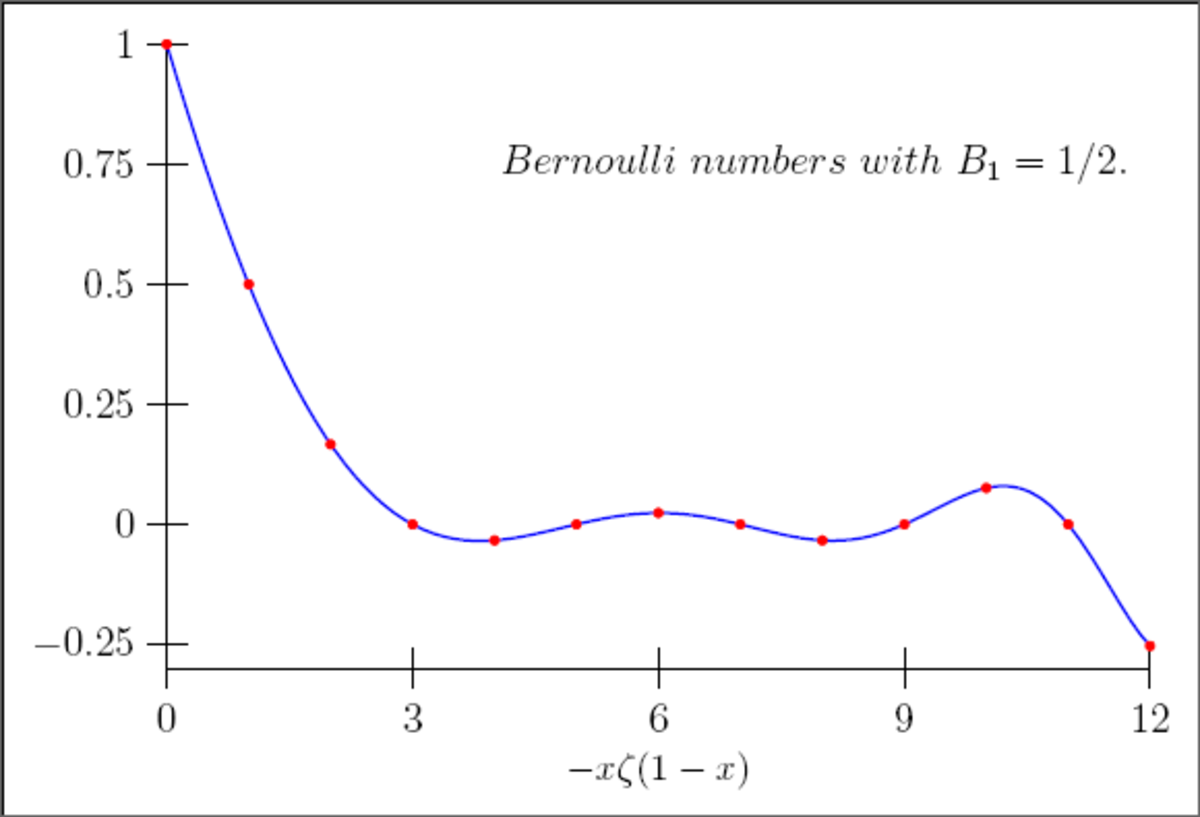
Les premiers nombres de Bernoulli sont les suivants :
|
|
À l'aide de la fonction génératrice, on peut démontrer que
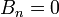
L'apparition de
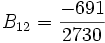
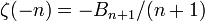
Applications en analyse
Les nombres de Bernoulli apparaissent dans le développement en série de Taylor des fonctions tangentes (circulaire et hyperbolique), dans la formule d'Euler-Maclaurin ainsi que dans des expressions de certaines valeurs de la fonction zêta de Riemann.
Identités remarquables
Leonhard Euler a obtenu la relation suivante entre les nombres de Bernoulli et la fonction zêta de Riemann :
Les relations suivantes, dues à Ramanujan, fournissent une méthode plus efficace pour le calcul des nombres de Bernoulli :
Une identité de Carlitz :
Propriétés géométriques
La formule de Kervaire-Milnor pour l'ordre du groupe cyclique des classes de difféomorphismes des (4n−1)-sphères exotiques qui bornent des variétés parallélisables pour
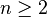
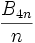
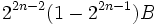
Propriétés arithmétiques
Il est possible d'exprimer les nombres de Bernoulli grâce à la fonction zêta de Riemann de la façon suivante :
-
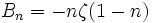
C'est la raison pour laquelle les nombres de Bernoulli possèdent des propriétés arithmétiques profondes, comme l'a découvert Kummer dans ses travaux sur le dernier théorème de Fermat.
Les propriétés de divisibilité des nombres de Bernoulli sont liées aux groupes des classes d'idéaux des corps cyclotomiques par un théorème de Kummer et son renforcement dans le théorème de Herbrand-Ribet, et aux nombres de classes des corps quadratiques par la congruence d'Ankeny-Artin-Chowla. Nous avons aussi un lien de parenté avec la K-théorie algébrique; si
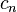
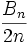
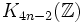
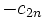
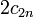
Le théorème de von Staudt-Clausen est aussi relié à la divisibilité. Il énonce ceci : si nous ajoutons
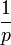
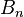
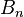
La conjecture d'Agoh-Giuga postule que p est un nombre premier si et seulement si
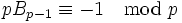
Continuité p-adique
Une propriété de congruence spécialement importante des nombres de Bernoulli peut être caractérisée comme une propriété de continuité p-adique. Si b, m et n sont des nombres entiers positifs tels que m et n ne sont pas divisibles par
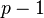
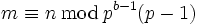
-
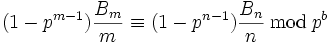
Puisque
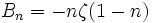
où