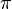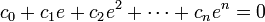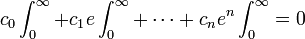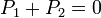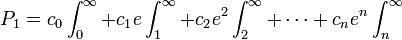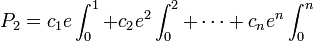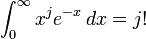Nombre transcendant - Définition
La liste des auteurs de cet article est disponible ici.
Esquisse de démonstration de la transcendance de e
La première démonstration que e est transcendant date de 1873. Nous suivrons maintenant la stratégie de David Hilbert (1862 - 1943) qui donna une simplification de la démonstration originale de Charles Hermite. L'idée est la suivante :
Supposons, dans le but de trouver une contradiction, que e est algébrique. Alors, il existe un ensemble fini de coefficients entiers
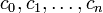
et c0 et cn sont tous deux différents de zéro.
Dépendant de la valeur de n, nous précisons un entier positif suffisamment grand k (pour nos besoin ultérieurs) et multiplions les deux côtés de l'équation ci-dessus par
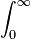
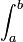
-
![\int^{b}_{a}:=\int^{b}_{a}x^{k}[(x-1)(x-2)\cdots(x-n)]^{k+1}e^{-x}\,dx\,](https://static.techno-science.net/illustration/Definitions/autres/1/14711a42cf8b99b6fa55cab24141308e_9603c5a563e3532a585c727c04e64611.png)
Nous arrivons à l'équation :
qui peut maintenant être écrite sous la forme
où
Le plan d'attaque maintenant est de montrer que pour un k suffisamment grand, les relations ci-dessus sont impossible à satisfaire parce que
-
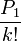
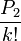
Le fait que
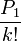
qui est valide pour tout entier positif j et peut être prouvé par récurrence au moyen d'une intégration par parties.
Pour montrer que
-
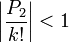
nous noterons d'abord que
![x^{k}[(x-1)(x-2)\cdots(x-n)]^{k+1}e^{-x}\,](https://static.techno-science.net/illustration/Definitions/autres/2/2ba7da49229818516d2f45b0de775a44_26a7c4f32bafdd379197c20523d02b79.png)
![[x(x-1)(x-2)\cdots(x-n)]^{k}\,](https://static.techno-science.net/illustration/Definitions/autres/e/e4111e47104eb5fa732fb159a47ebe08_cc870812f99354f3f43a58f3bc4100f9.png)
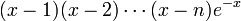
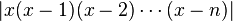
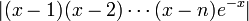
-
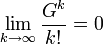
est alors suffisant pour achever la démonstration.
Une stratégie similaire, différente de l'approche originale de Lindemann, peut être utilisée pour montrer que le nombre
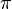
Pour des informations détaillées concernant les démonstrations de transcendances de