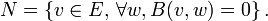Noyau (algèbre) - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Noyau d'une forme quadratique
Sur un espace vectoriel réel E, une forme quadratique est une application polynomiale
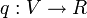
-
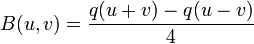
Le noyau de q est le sous-espace vectoriel
La contraction de B par v désigne l'application linéaire
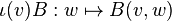
-
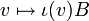
L'image est un sous-espace vectoriel de l'espace dual E * qui est l'annulateur du noyau N.
Noyau d'un morphisme de corps
Le noyau d'un morphisme de corps (c'est-à-dire un morphisme d'anneau où les anneaux considérés sont des corps) est toujours réduit à l'élément neutre 0, de sorte que tout morphisme de corps est injectif.
Noyau en général
Toutes ces notions de noyaux se généralisent dans le cadre de la théorie des catégories abéliennes.