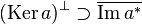Opérateur adjoint - Définition

Espace de Banach

Comparer avec l'article anglais en:Unbounded operator

De nombreuses propriétés, valables pour les Hilbert peuvent être généralisées. L'analyse de l'adjoint d'un opérateur dans le cadre plus général des Banach possède des analogies certaines avec le cas précédent. Les techniques utilisées sont néanmoins un peu différentes. Dans ce paragraphe E et F désignent des Banach et a un opérateur non borné de E dans F.

Le terme opérateur non borné désigne une application linéaire sans précision sur le caractère continu de l'opérateur. Le mathématicien Haïm Brezis précise : Il peut donc arriver qu'un opérateur non borné soit borné. La terminologie n'est pas très heureuse, mais elle est communément répandue et elle n'engendre pas de confusion !

Existence et unicité

Comme précédemment, tout opérateur a admet un unique adjoint. Plus précisément :

• Pour tout opérateur non borné a de D(a) dans F il existe un unique adjoint, et l'adjoint est linéaire.

La question se pose alors de savoir si D(a^*) est dense dans le dual de F.

• Si a est un opérateur fermé, alors pour la topologie faible du dual de F, D(a^*) est dense dans le dual de F. Si de plus F est reflexif alors D(a^*) est dense pour la topologie usuelle.

• Pour tout opérateur non borné a de D(a) dans F il existe un unique adjoint, et l'adjoint est linéaire.

Remarquons dans un premier temps que D(a^*) est un espace vectoriel. Soit y₁^* (resp. y₂^*) un vecteur de D(a^*), λ un élément de K et c₁ (resp. c₂) une constante vérifiant la propriété suivante :

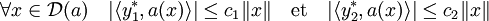
La majoration suivante montre que y₁^* + λy₂^* est bien élément de D(a^*).

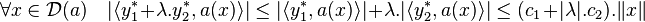
Soit y^* un élément de D(a^*). Par défaut, a^*(y^*) est une forme linéaire continue sur D(a). L'ensemble d'arrivé K est complet la forme est continue donc uniformément continue et se prolonge par continuité de manière unique (cf l'article Continuité uniforme). Ainsi, l'application a^*(y^*) est bien un élément de E^*.

La linéarité de a^* provient directement de la bilinéarité de <.,.>.

 

Continuité de l'adjoint

Le théorème du graphe fermé indique qu'un opérateur a est continu si et seulement si son graphe est fermé. Le graphe de a est le sous-espace vectoriel de ExF formé des points (x, a(x)) quand x parcourt D(a). Un opérateur ayant un graphe fermé est dit fermé, ce qui revient à dire borné ou continue. Pour une raison de style, il est plus fréquent de parler d'un opérateur non borné fermé que d'un opérateur non borné borné, même si les significations sont identiques.

• Un opérateur non borné a à domaine dense possède un adjoint fermé.

La démonstration est relativement simple. Soient (v_n^*) une suite de D(a^*) convergente vers v^* dans le dual de F et tel que la suite (a^*(v_n^*)) converge aussi, mais cette fois-ci vers u^* dans le dual de E. L'objectif est de montrer que (v^*, u^*) est un élément du graphe de l'adjoint de a. L'égalité suivante est vérifiée :

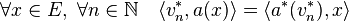
Un passage à la limite montre que :

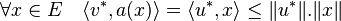
La dernière majoration montre que v^* est un élément de D(a^*) et la dernière égalité montre que u^* est l'image de v^* par a^*. En conséquence le point (v^*, u^*) est un élément du graphe de a^*, ce qui démontre la proposition.

 

Orthogonalité

Si a est fermé et possède un domaine dense, alors les propriétés d'orthogonalités correspondant à la situation hilbertienne restent vraies :

• Le noyau de a est égal à l'orthogonal de l'image de a^* et le noyau de a^* est égal à l'orthogonal de l'image de a.

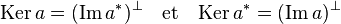
La situation diffère légèrement pour l'orthogonal des noyaux.

• L'orthogonal du noyau de a contient l'adhérence de l'image de l'adjoint de a et l'orthogonal du noyau de l'adjoint de a est l'adhérence de l'image de a.

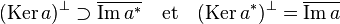
Si l'espace E est réflexif, alors l'orthogonal du noyau de a est égal à l'adhérence de l'image de a^*, dans le cas contraire, l'égalité n'est pas assurée.

Avec les hypothèse de fermeture et de densité du domaine de a :

• Les quatre propriétés suivantes sont équivalentes :

(1) L'image de a est fermée.

(2) L'image de l'adjoint de a est fermée.

(3) L'image de a est l'orthogonal du noyau de l'adjoint.

(4) L'image de l'adjoint est l'orthogonal du noyau de a.

• Le noyau de a est égal à l'orthogonal de l'image de a^* et le noyau de a^* est égal à l'orthogonal de l'image de a :

On remarque que, comme a est continue, le domaine de a^* est le dual de F entier, donc :

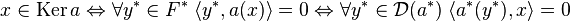
Ce qui démontre la première égalité.

On remarque que, comme D(a) est dense dans E, un vecteur du dual de E est nul si et seulement s'il est orthogonal à D(a), donc :

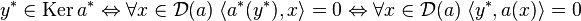
Ce qui démontre la deuxième égalité.

• L'orthogonal du noyau de a contient l'adhérence de l'image de l'adjoint de a et l'orthogonal du noyau de l'adjoint de a est l'adhérence de l'image de a :

L'étude des formes bilinéaires continues montre que l'orthogonal d'un d'orthogonal d'un espace vectoriel contient l'adhérence de l'espace initiale. L'orthogonal de l'orthogonal de l'image de d'adjoint de a contient donc l'adhérence de l'image de l'adjoint de a. La proposition précédente permet de conclure pour l'inclusion suivante :

 

Surjectivité

Conséquence de la continuité de a