Opérateur adjoint - Définition
La liste des auteurs de cet article est disponible ici.
Espace de Hilbert
On suppose dans toute cette section que H est un espace de Hilbert, c'est-à-dire un espace préhilbertien complet. Dans ce cas, le dual topologique s'identifie avec l'espace H. Les résultats obtenus dans le cas des formes bilinéaires s'appliquent sans beaucoup de modifications.
Le cas de la dimension finie est un peu plus simple car toute application linéaire est continue et l'isomorphisme entre l'espace et son dual est plus évident. Une approche plus didactique est disponible dans l'article Espace euclidien pour le cas réel et Espace hermitien pour le cas complexe.
Remarque : Dans le cas où le corps sous-jacent à H est celui des complexes, le produit scalaire est sesquilinéaire. La convention choisie dans l'article est que la forme est linéaire pour la première variable et antilinéaire pour la seconde. Le conjugué d'un scalaire λ est noté
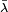
Existence (et unicité)
En effet, soit a un opérateur borné. Soit y un vecteur de H, l'application qui à un vecteur x associe <a(x)|y> est une forme linéaire continue. Le théorème de représentation de Riesz garantit alors l'existence d'un (unique) vecteur z tel que cette forme linéaire continue coïncide avec l'application qui à x associe <x|z>. L'application a* qui à y associe z est alors l'adjoint de a.
-
- Réciproquement, si deux applications quelconques
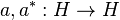
- Réciproquement, si deux applications quelconques
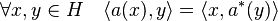
alors
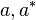
Montrons-le par exemple pour a * . La linéarité est une conséquence directe des propriétés de bilinéarité et de non dégénérescence du produit scalaire. On utilise que :
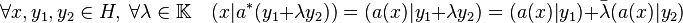
On en déduit :
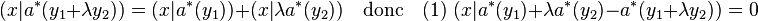
L'égalité (1) est vraie pour toutes les valeurs de x ce qui montre que le terme de droite est nul. Cette nullité démontre le caractère linéaire de a*.
Pour montrer la continuité de a * il suffit, grâce au théorème du graphe fermé, de vérifier que si xn tend vers x et si a*(xn) tend vers y alors a*(x)=y. Or ces deux hypothèses impliquent (en utilisant l'équation d'adjonction) que pour tout z,
Propriétés élémentaires
A beaucoup d'égards l'adjoint est une image miroir de l'opérateur.
-
- L'adjoint de l'opérateur a est linéaire.
Ce résultat (qui ne fait pas intervenir la linéarité de a) a été démontré plus haut.
En dimension finie, la matrice de l'adjoint est égale à la transposée de la matrice conjuguée de a. La démonstration est une fois encore simple, soit A la matrice de a dans une base de H et X (resp. Y) la matrice d'un vecteur x (resp. y) de H.
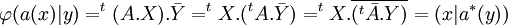
Le terme borné signifie ici que l'image de la boule unité est bornée. Un opérateur est borné si et seulement s'il est continu.
La continuité de l'adjoint a été démontrée plus haut sans supposer que a était borné, à l'aide du puissant théorème du graphe fermé. Sous l'hypothèse que a est borné, la preuve est plus élémentaire : il suffit de remarquer que la norme de a ainsi que celle de l'adjoint est celle de la forme bilinéaire ou sesquilinéaire qui à x et y associe (a(x) | y) = (x | a*(y)).
-
- La norme de la composée de a et de son adjoint est égal au carré de celle de a :
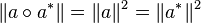
Orthogonalité
Les propriétés d'orthogonalités associées aux formes bilinéaires sont présentes dans ce contexte :
-
- Le noyau de a est égal à l'orthogonal de l'image de a* et le noyau de a* est égal à l'orthogonal de l'image de a.
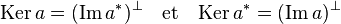
La démonstration est immédiate, elle provient de la chaîne d'équivalences suivante :
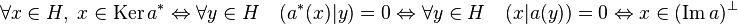
Un corollaire immédiat est qu'en dimension finie a et a* ont même rang car l'orthogonal d'un espace vectoriel fermé est un supplémentaire. En cas de dimension infinie, si a est injective, alors a* possède une image dense dans H, ce qui ne signifie pas que a* est surjective.
Une démonstration analogue permet d'établir le résultat suivant :
-
- L'orthogonal du noyau de a est égal à l'adhérence de l'image de l'adjoint de a. De même, l'adhérence de l'image de a est l'orthogonal du noyau de l'adjoint.
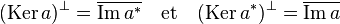
L'adhérence d'un ensemble E est le plus petit fermé qui le contient, il est ici noté
-
- Soit E un sous-espace stable par a, l'orthogonal de E est stable par a*.
La démonstration est de même nature que la précédente. Soit y un élément de l'orthogonal de E, son image par a* est orthogonal à E.
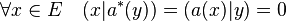
Application adjointe
Il est possible de considérer l'application * de L(H) dans lui-même, qui à l'opérateur a associe l'adjoint a*. Cette fonction est dénommée l'application adjointe.
L'espace de départ L(H) dispose non seulement d'une structure d'espace vectoriel mais aussi d'algèbre associative avec pour multiplication interne la loi de composition. Il est possible de considérer une autre multiplication interne

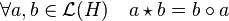
L'espace L(H)op désigne l'algèbre L(H) munie de la multiplication

-
- L'application adjointe est un isomorphisme isométrique antilinéaire d'algèbre de L(H) dans L(H)op.
Dire que l'application adjointe est un isomorphisme d'algèbre revient à dire, qu'en plus de la conservation de la linéarité, la propriété suivante est vérifiée :
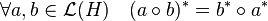
-
- L'application adjointe est involutive.
Cette propriété signifie que :
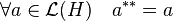
En dimension finie, une involution est une symétrie, c'est-à-dire un endomorphisme diagonalisable de valeurs propres 1 et -1, d'espaces propres associés deux espaces supplémentaires. Cette propriété est générale sur tous les Hilbert.
-
- L'espace L(H) admet deux sous-espaces supplémentaires espaces propres pour l'application adjointe de valeurs propres 1 et -1. Un vecteur propre de valeur propre associée 1 (resp. -1) est appelé autoadjoint (resp. antisymétrique).
-
- En dimension finie l'espace propre de valeur propre associée 1 (resp. -1) est de dimension n(n + 1)/2 (resp. n(n - 1)/2) si n désigne la dimension de H.
En dimension finie et si le corps K est celui des complexes, les endomorphismes autoadjoints et antisymétriques sont diagonalisables, c'est-à-dire qu'il existe une base de E de vecteurs propres. Cette propriété est vraie pour tous les endomorphismes normaux, c'est-à-dire ceux qui commutent avec leur adjoint. Les automorphismes orthogonaux sont normaux et donc diagonalisable.
Si le corps K est celui des réels, les endomorphismes autoadjoints sont toujours diagonalisables.
-
- L'application adjointe est un isomorphisme isométrique antilinéaire d'algèbre de L(H) dans L(H)op :
L'antilinéarité découle directement du caractère sesquilinéaire du produit scalaire :
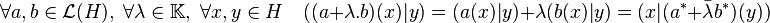
La conservation de la multiplication interne se démontre de manière analogue :
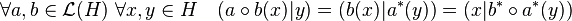
-
- L'application adjointe est involutive :
Cette propriété est la conséquence du caractère hermitien du produit scalaire :
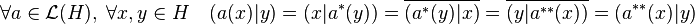
-
- L'espace L(H) admet deux sous-espaces supplémentaires espaces propres pour l'application adjointe de valeurs propres 1 et -1 :
Considérons l'application pde L(H) dans lui-même qui à un opérateur a associe 1/2(a + a*). Cette application est une projection sur l'espace des opérateurs autoadjoints parallèlement à l'espace des antisymétriques. Les propriétés des projecteurs permettent de conclure.
-
- En dimension finie l'espace propre de valeur propre associée 1 (resp. -1) est de dimension n(n + 1)/2 (resp. n(n - 1)/2) si n désigne la dimension de H :
Considérons l'application de L(H) dans l'ensemble L2(H) l'espace des formes sesquilinéaires. Cette application est un isomorphisme qui envoie l'espace des autoadjoints (resp. antisymétriques) sur les formes symétriques (resp. alternées). Comme les formes symétriques (resp. alternées) forment un espace vectoriel de dimension n(n + 1)/2 (resp. n(n - 1)/2) la proposition est démontrée.
Remarque : Plus de détails sont donnés dans l'article Forme bilinéaire.
Spectre
Le spectre d'un opérateur a est l'ensemble des scalaires λ tel que l'application a - λ.Id ne soit pas bijective (Id désignant l'application identité). En dimension finie le spectre est l'ensemble des valeurs propres. En dimension infinie il peut être plus large (voir les articles Spectre d'un opérateur linéaire et Valeur spectrale).
-
- Le spectre de l'opérateur a* est le conjugué de celui de a.
Les propriétés du spectre se précisent si H est de dimension finie :
-
- Si H est de dimension finie, le déterminant (resp. le polynôme caractéristique) de a* est le conjugué de celui de a.
-
- Si H est de dimension finie, le polynôme minimal de a* est le conjugué de celui de a.
En conséquence, si λ est valeur propre de multiplicité m de l'opérateur a (c'est-à-dire racine d'ordre m de son polynôme caractéristique) alors le conjugué de λ est valeur propre de multiplicité m de l'opérateur a*, et de même, si λ est racine d'ordre m du polynôme minimal de a (ce qui équivaut à dire que m est le plus petit entier tel que le noyau de (a -λId)m soit égal au noyau de (a -λId)m+1), alors le conjugué de λ est racine d'ordre m du polynôme minimal de a*.
-
- Le spectre de l'opérateur a* est le conjugué de celui de a :
Un opérateur est bijectif si et seulement si son adjoint l'est (d'après la propriété
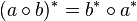
-
- Si H est de dimension finie, le déterminant (resp. le polynôme caractéristique) de a* est le conjugué de celui de a :
L'article Déterminant (mathématiques) démontre qu'une matrice carrée possède le même déterminant que sa transposée. De plus, le déterminant d'une matrice conjuguée est le conjugué du déterminant. Le fait que le déterminant d'un endomorphisme soit égal à celui de sa matrice montre que le déterminant de l'adjoint de a est le conjugué de celui de a. Les mêmes propriétés appliquées à l'endomorphisme a - λId montrent l'égalité des polynômes caractéristiques.
-
- Si H est de dimension finie, le polynôme minimal de a* est le conjugué de celui de a :
Soit P(X) le polynôme minimal de a. L'endomorphisme P(a) est nul et son conjugué l'est aussi, ce qui montre que le polynôme conjugué de P(X) annule l'adjoint, son conjugué est donc un multiple du polynôme de a*. On montre de même que le polynôme conjugué du polynôme minimal de l'adjoint annule a. Les deux polynômes sont multiples l'un de l'autre, ils sont tous deux unitaires, ce qui permet de conclure à l'égalité.

















































