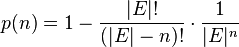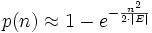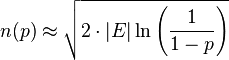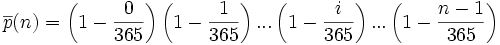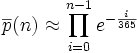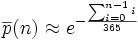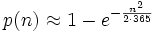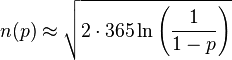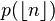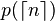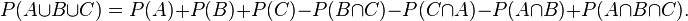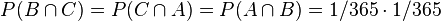Paradoxe des anniversaires - Définition

Généralisation

Ce paradoxe des anniversaires se généralise à la situation plus abstraite que l'on peut énoncer sous la forme :

Soit E un ensemble fini. La probabilité p(n) que, parmi n éléments de E, chaque élément étant tiré uniformément dans tout l'ensemble E, deux éléments au moins soient identiques vaut :

où la notation | E | désigne le nombre d'éléments de l'ensemble E.

Une valeur approchée est donnée par

et une valeur de n en fonction de p par

Approximation

p(n)

La probabilité peut se réécrire sous la forme :

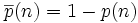
Or, on a le développement limité e^x = 1 + x + o(x) pour x voisin de 0. Cela conduit à l'approximation :

Or, la somme des entiers de 0 à n − 1 vaut (n − 1)n / 2, ce qui donne finalement :

En revenant à p(n) :

n(p)

L'approximation de p(n) permet d'obtenir simplement une approximation du nombre de personnes nécessaire pour avoir une probabilité donnée p d'avoir au moins deux personnes avec le même jour d'anniversaire. On obtient ainsi :

Quelques valeurs numériques

Le tableau ci-dessous indique, pour une probabilité p, l'approximation n(p), puis, sur la même ligne, l'approximation de la probabilité pour l'entier inférieur ou égal à n(p) (noté ) et celle de probabilité pour l'entier supérieur ou égal à n(p) (noté ). Normalement, la probabilité p fixée au départ doit être comprise entre ces deux valeurs. Les entrées ne vérifiant pas cette condition sont signalées en couleur.

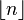
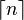
p	n
0,01	2,70864	2	0,00274	3	0,00820
0,05	6,11916	6	0,04046	7	0,05624
0,1	8,77002	8	0,07434	9	0,09462
0,2	12,76302	12	0,16702	13	0,19441
0,3	16,13607	16	0,28360	17	0,31501
0,5	22,49439	22	0,47570	23	0,50730
0,7	29,64625	29	0,68097	30	0,70632
0,8	34,27666	34	0,79532	35	0,81438
0,9	40,99862	40	0,89123	41	0,90315
0,95	46,76414	46	0,94825	47	0,95477
0,99	57,98081	57	0,99012	58	0,99166

Paires trompeuses

Lorsqu'on effectue le calcul par intuition, en comptant le nombre de paire, on omet le fait que les évènements ne sont pas disjoints.

Prenons l'exemple pour trois personnes (Alain, Bernard et Charles). En les prenant deux à deux, la probabilité d'avoir la même date d'anniversaire est 1/365. Et donc pour les trois paires, on aurait 3/365. Cependant, en faisant ce calcul, on oublie que l'anniversaire des trois personnes peut avoir lieu le même jour. Définissons trois évènements : A: Alain et Bernard ont leur date d'anniversaire en commun B: Bernard et Charles ont leur date d'anniversaire en commun C: Charles et Alain ont leur date d'anniversaire en commun. Et donc, P(A) = P(B) = P(C) = 1 / 365. Ce que nous cherchons c'est la probabilité d'avoir l'évènement A ou B ou C, soit . En utilisant le formalisme repris dans les axiomes des probabilités.

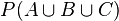
Comme les éléments sont indépendants deux à deux (le fait que Charles ait son anniversaire le même jour que Bernard n'a pas d'influence sur le fait qu'il ait aussi son anniversaire en même temps qu'Alain) donc

Par contre, on peut réécrire . Or ici, A et ne sont pas indépendants, si Bernard et Charles ont leur anniversaire en même temps et Charles et Alain aussi, alors forcément Alain et Bernard aussi, donc .

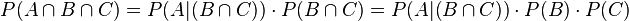
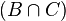
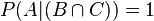
En résumé, on aura . Ce qui correspond bien au résultat précédent.

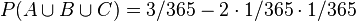
Etendre ce raisonnement à un plus grand nombre de personnes devient rapidement très compliqué. Cependant, on comprend mieux pourquoi il ne suffit pas d'avoir 28 personnes pour être certain d'avoir un anniversaire commun.