Paradoxe des anniversaires - Définition

Anecdote

Dans Le Livre qui rend fou, Raymond Smullyan raconte que lui-même a fait établir la formule à ses 19 élèves. Il conclut après application numérique qu'il y a nettement moins d'une chance sur deux (un peu moins de 38%) pour que deux élèves aient leur anniversaire le même jour. Un élève lui répond qu'il parie que c'est tout de même le cas. Le professeur fait l'appel en demandant aux élèves de donner leur date de naissance, et éclate de rire avant la fin, suivi de toute la classe, en se souvenant que deux de ses élèves sont jumeaux.

Applications

Dans Le Trésor des Paradoxes (Éd Belin, 2007), les auteurs notent que l’informaticien américain Robert Mac Eliece a établi l'intérêt du paradoxe des anniversaires en informatique, pour s’assurer de la fiabilité des mémoires d’ordinateur, grâce à des codes détecteurs d’erreurs, fondés notamment sur les travaux de Richard Hamming aux Laboratoires Bell. La stratégie des codes détecteurs d’erreurs s’avère, du point de vue statistique, similaire au paradoxe des anniversaires. Le paradoxe des anniversaires est utilisé en cryptographie pour élaborer des attaques sur les fonctions de hachage. Une des contraintes imposées sur ces fonctions, pour une utilisation cryptographique, est de produire peu de collisions, autrement dit, de rarement prendre la même valeur sur des entrées différentes.

Le paradoxe des anniversaires donne une borne sur le nombre moyen d'éléments nécessaires pour avoir une collision avec une probabilité , à savoir essentiellement la racine carrée du nombre de valeurs possibles pour la fonction de hachage, sous l'hypothèse que cette fonction est uniformement distribuée sur ses valeurs d'arrivée.

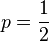
Plus concrètement, si une fonction de hachage a une sortie de N bits alors l'ensemble d'arrivée possède 2^N éléments et il faut environ hachés d'éléments distincts pour produire une collision avec 50 % de chance ; les sorties de la fonction pouvant être comparées à des personnes avec des anniversaires se répartissant sur 2^N valeurs.